We read with interest the article by Cantón et al1 in the April 2005 issue of the AJNR reporting on intra-aneurysmal pressure changes during HydroCoil embolization.
The authors studied the intra-aneurysmal pressure after using hydrogel-coated coils. The intra-aneurysmal pressure was measured by using a standard pressure microprobe placed in a silicone model of a basilar tip aneurysm subjected to pulsatile flow.
Once hydrogel-coated coils are placed within a liquid substance, they tend to swell, similar to the behavior of polymers in a diaper material. Thus, hydrogel-coils depending on the number of cross-links within the polymer and the amount of coils used will incorporate or replace most of the blood within the aneurysm sac.
In trying to address some important biomechanical aspects with the use of HydroCoils, the authors were interested to study fluid pressure changes related to coiling. Of greater interest is to understand the risk of rupture associated with coiling aneurysms. This would include rather a measurement of the wall stress. The authors briefly address this shortcoming of their study.
The degree of stress to which an aneurysm wall is subjected is related to the aneurysm volume. For elastic material Laplace’s law defines the relationship between wall tension (eg, in a balloon), internal fluid pressure, and radius or volume. That is, without fluid pressure changes there will be no changes in wall tension. In an aneurysm an acute volume increase and stretching of the aneurysm wall can of course occur as a result of overpacking an aneurysm with solid material, or as in this study with the use of HydroCoils. In addition local deflection of the wall, resulting in increased wall stress, can also result directly from using a stiffer material such as a coil. Wall stress in an aneurysm can be measured, but is much more complicated than measuring the intra-aneurysmal fluid pressure. To measure the stress at the aneurysm wall, smaller probes (spring elements) have in the past been placed over the aneurysm surface. The applied force during coiling and its distribution can be monitored and plotted over the entire surface.
The authors’ main goal was to study the intra-aneurysmal total fluid pressure changes during placement of HydroCoils. The total intra-aneurysmal fluid pressure (or any pressure within the vascular tree) is the sum of static pressure and dynamic pressure as described by the Bernoulli equation. Dynamic pressure at any point in an artery is the amount of pressure required to arrest flow, and in the larger arteries is a very small fraction (single percents) of the total pressure. The major component of the total pressure is the static pressure that is the difference between the total and the dynamic pressure. In an aneurysm, however, flow is generally slower than in the parent vessel and the static pressure is nearly equivalent to the total pressure and thus, a measurable pressure rise in an aneurysm should not be expected. An intra-aneurysmal pressure increase can be expected only if the aneurysm would be isolated completely from the parent vessel during coiling.
Flow into side branches or within an artery is maintained by an arterial-to-venous pressure gradient, otherwise known as pressure-driven flow. The driving force for blood to enter an aneurysm is sustained by parent vessel flow pulsatility and the exchange of momentum between the parent artery and aneurysm. Because an unruptured aneurysm does not have a low-pressure exit port, it cannot be considered as a pressure-driven flow. These are basic principles in fluid mechanics applied to parent artery/aneurysm complex. In fact, some recent work from Sorteberg et al2 confirm these well-known facts among mechanical engineers. Thus, placement of coils or a porous stent across the neck of an aneurysm will not change the intra-aneurysmal pressure; however, the flow field will change. The vortices within the aneurysm will decrease. In a non-Newtonian fluid such as blood, the apparent viscosity will increase as a result of decreased shear rate. A stent or coils may uncouple the momentum exchange by disrupting the flow at the interface (neck) between artery and the aneurysm without changing the pressure.
In summary, a change in intra-aneurysmal fluid pressure should not be expected after treating an aneurysm with coils or a porous stent material. The more interesting question may be whether certain coils, such as HydroCoils, may increase the wall stress of the aneurysm, which then potentially could lead to (re)rupture. The authors, however, need to address the question by using different methods, as reflected in the references detailed at the bottom of this letter.3–7
Changes of Intra-Aneurysmal Pressure during Coiling
Reply:
We appreciate the interest of Drs. Wakhloo and Lieber in our study.1 They raise an interesting question concerning the theoretical clinical issue of (re)rupture after packing aneurysms with HydroCoils and suggest further measurements of the resulting wall stresses.
The aim of our study was to investigate the possibility of an increase in the intra-aneurysmal fluid pressure after the full expansion of the gel. The deployment of the coils can create fluid pockets along the aneurysmal wall that could potentially be pressurized after the complete expansion of the gel. Our measurements show that, when the fully hydrated coils occupy 93% of the total volume of the aneurysmal sac, there is no such increase in the fluid pressure, which indicates that the fully expanded HydroCoil system behaves like porous media that will not lead to an increase in the wall tension. Furthermore, we have not observed any expansion of the gel outside the aneurysmal neck or measured any deformation at the neck that could indicate that the expansion of the gel is exerting a force on the aneurysmal wall.
After complete hydration of the coils, the decrease in fluid velocity inside the sac due to the low porosity of the mesh packing the aneurysm would lead, in turn, to the formation of thrombus, which would occupy the open spaces. We were unable to achieve this condition in our experiments because we did not use blood in our in vitro study. We can show, however, that if a clot is formed the wall tension decreases.
We have performed numerical simulations by using a finite element solver (FEMLAB; Comsol, Burlington, Mass) to answer Drs. Wakhloo and Lieber’s concerns. We have computed the fluid pressure for different packing degrees, assuming that the coils behave as porous media, to compare with our experimental results. We have also computed the Von Mises stresses acting on the wall of the aneurysm before and after full occlusion of the aneurysmal sac.
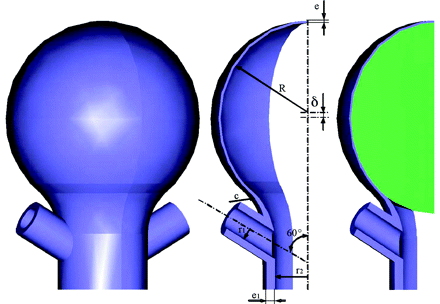
Figure 1 shows the aneurysm geometry and characteristic lengths. Two different values for the eccentricity of the aneurysmal sac are considered to study the effect of the thickness variation on the wall tension. Zero eccentricity (δ) corresponds to uniform thickness along the aneurysmal wall, whereas higher values correspond to the fundus being thinner than the neck. Because of the symmetry of the model, the simulations are made only for one quarter of the aneurysmal sac.
The pressure and velocity fields are computed for different degrees of porosity (φ) and are plotted in Fig 2. The conditions used for these calculations are the following: The mean value of the inlet velocity is 0.2 m/s, and the outlet pressure is 1000 Pa. Blood is assumed to be a Newtonian fluid with density of 1000 kg/m3 and viscosity of 0.004 Pa·s. The vessel wall is assumed to be rigid, and no-slip condition was applied. With no packing, the velocity and pressure fields are computed solving the Navier-Stokes equations for the whole domain (regions 1 and 2). When packing the aneurysm with coils, however, the flow in the aneurysmal sac (region 2) is computed by solving Darcy’s law. The coil-filled sac is assumed to behave as a fibrous medium, with an isotropic permeability (K). The permeability depends on the radius of the fiber (2 × 10−4 m) and the porosity. The porosities used in this study were K = 1.4 × 10−9 m2 for φ = 50, and K = 4.5 × 10−13 m2 for φ = 0.05, following Boutin’s findings.2
No significant difference (<2%) is observed in the intra-aneurysmal fluid pressure with increasing level of packing, a result consistent with our experimental measurements,1 even though the velocity magnitude is considerably reduced. For example, the velocity is 10 times lower when the porosity is 0.5.
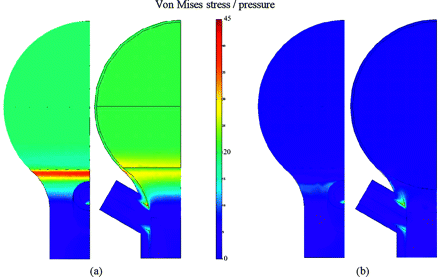
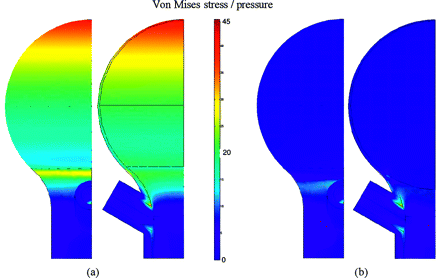
To investigate the possible increase in the wall tension after complete filling of the aneurysmal sac, we have computed the Von Mises stresses for 2 different values of the thickness at the aneurysmal fundus (Figs 3 and 4). The material of the wall is assumed to be isotropic linear-elastic, with an elastic modulus of 2 MPa and Poisson ratio of 0.4. The pressure applied on the wall, P, is constant and taken equal value to the typical systolic pressure of 125 mm Hg.
Figure 3A shows that the ratio between the Von Mises stress and the pressure along the aneurysmal wall is constant, except for the neck, and its value is of the same order as Laplace’s law’s estimation, σ/P ≈ 20. With no uniform thickness in the aneurysmal sac (Fig 4A), however, the Von Mises stress is not constant, with the maximum value now located at the fundus. This value is also of the same order as the Laplace’s law’s estimation for the thickness at the fundus, σ/P ≈ 40.
Figures 3B and 4B show the ratio between the Von Mises stress and the pressure corresponding to the complete filling of the sac. In these calculations, the full expanded coils are described as an elastic isotropic material with an elastic modulus of 0.5 MPa corresponding to the gel properties. The full occlusion of the sac reduces the Von Mises stress independently of the wall thickness. We have chosen these 2 cases (no treatment and 100% occlusion) because the actual Von Mises stresses for any packing degree should be a value somewhere between them.
In summary, we have shown that the hydration of the coils, up to 93% volume filling, does not lead to an increase in the Von Mises stresses acting on the aneurysm wall. Our original measurements1 and the results presented here are consistent with the filling characteristics of the HydroCoil reported by others (73% for HydroCoil vs 32% for platinum3,4).
A, Aneurysm geometry. B, Characteristic lengths: R = 4 mm; e1 = 0.3 mm; r1 = 0.5 mm; r2 = 1.6 mm; C = 2 mm. Case 1: e = 0.1 mm; δ = 0 mm. Case 2: emini = 0.05 mm; δ = 0.05 mm. C, Aneurysm with 100% coil filling.
Numerical results deduced from simulations of the flow through the aneurysm with various packing of coils. A, φ = 1 (no coil). B, φ = 0.5. C, φ = 0.05. Because of the symmetry of the model, the numerical results are shown for only one quarter of the sac.
Evolution of the ratio Von Mises stress/pressure. Case 1: e = 0.1 mm; δ = 0 mm. A, Aneurysm without coil. B, Aneurysm with 100% coil filling.
Evolution of the ratio Von Mises stress/pressure. Case 2: emini = 0.05 mm; δ = 0.05 mm. A, Aneurysm without coil. B, Aneurysm with 100% coil filling.
- Copyright © American Society of Neuroradiology