Advertisement
Research ArticleBRAIN

Effects of Number of Diffusion Gradient Directions on Derived Diffusion Tensor Imaging Indices in Human Brain

H. Ni, V. Kavcic, T. Zhu, S. Ekholm and J. Zhong
American Journal of Neuroradiology September 2006, 27 (8) 1776-1781;

Abstract

BACKGROUND AND PURPOSE: The effects of a number of diffusion-encoding gradient directions (NDGD) on diffusion tensor imaging (DTI) indices have been studied previously with theoretic analysis and numeric simulations. In this study, we made in vivo measurements in the human brain to compare different clinical scan protocols and to evaluate their effects on the calculated DTI indices.

METHODS: Fifteen healthy volunteers were scanned with a 1.5T MR scanner. Single-shot DTI images were acquired using 3 protocols different in NDGD and number of excitations (NEX) for each direction (NDGD/NEX = 6/10, 21/3, 31/2). Means and standard error of mean (SEM) were calculated and compared in 6 regions of interest (ROIs) for mean diffusivity (〈D〉), fractional anisotropy (FA), diffusion tensor eigenvalues (λ1, λ2, and λ3), and correlation coefficients (r) of these indices among the 3 DTI protocols.

RESULTS: At the ROI level, no significant differences were found for the mean and SEM of 〈D〉 and FA among protocols (P > .05). The 6-NDGD protocol, however, yielded higher values for λ1 and λ2 and lower values for λ3 in most ROIs (P < .05) compared with the other protocols. At the voxel level, the correlation between the protocols r21–31 were higher than r6–21 and r6–31 in most ROIs. The correlation of FA among 3 protocols also increased with increasing anisotropy.

CONCLUSION: For ROI analyses, different NDGDs lead to similar values of FA and 〈D〉 but different eigenvalues. However, different NDGDs at the voxel level provide varying values. The selection of the NDGD, therefore, should depend on the focus of different DTI applications.

With MR diffusion tensor imaging (DTI), diffusion anisotropy can be quantified, and subtle white matter (WM) changes that are not normally seen on conventional MR imaging can be detected. DTI has been applied in various diseases, such as Alzheimer disease (AD),1–4 multiple sclerosis (MS),5–15 and HIV infections,16–18 to monitor and assess WM changes.

There are some basic requirements in clinical applications of DTI. For example, the total scan time cannot be too long, relatively thin sections are required for accurate depiction of structures, and a sufficient number of sections is needed to cover the entire brain. Optimization of the DTI acquisition protocols is needed with regard to the above limitations and requirements. One of the most important factors in DTI acquisition is the number of diffusion-encoding gradient directions (NDGD). At least 6 diffusion-weighted (DW) images for every section (ie, NDGD = 6) are needed to calculate the diffusion tensor (D), and all DTI indices are calculated from D. As NDGD increases, more DW images are used for the calculation of D, resulting in more accurate D estimation. Alternatively, more averaging of each DW image also results in a higher signal-to-noise ratio (SNR) and improved estimation of D. However, both methods require a longer scan time. In most clinical reports (e.g., on AD studies), diffusion-encoding gradients were applied in only 6 directions.1–3 As the scanner hardware has improved rapidly in recent years, use of more DW directions has become more popular. For example, in 1 study, 30 directions were used.4

There is still no clear conclusion about different schemes for selection of NDGD and number of excitations (NEX) for the evaluation of DTI indices. Some researchers19,20 claim that using more than 6 DW gradient directions provides better measures of the D than the conventional 6 directions. In 1 study, no advantage in the use of more than 6 sampling orientations was shown as long as the selected orientations point to the vertices of an icosahedron.21 Another study22 determined that the minimum number of unique encoding directions required for robust anisotropy estimation is between 18 and 21. A recent study with Monte Carlo simulations23 concluded that at least 20 unique sampling orientations were necessary for a robust estimation of anisotropy, whereas at least 30 unique sampling orientations were required for a robust estimation of tensor orientation and mean diffusivity. The error propagation on effects of NDGD and b value on fractional anisotropy (FA) were recently investigated by theoretic analysis,24 and the results suggested an increase in error propagated to calculate FA as NDGD decreased. To our knowledge, no experimental studies have investigated the effects of various NDGDs on DTI measurements in vivo.

The purpose of this work was to compare DTI protocols with combinations of various NDGD and various numbers of images. The effects of the number of diffusion gradient directions on the calculated DTI indices were analyzed under typical clinical conditions, and suggestions were made for more reliable DTI protocol designs. The main goal of our study was to test, in humans, previous results from simulation studies, primarily based on the study of Jones,23 which determined “cutoffs” of DTI reliability at specific NDGDs of 20 and 30 for FA and Trace, respectively. Consequently, NDGD = 6 (a very commonly used protocol) and NDGD = 21 and 31 were used in different acquisitions in the present study.

In recent clinical applications, in addition to the compound indices (such as mean diffusivity [〈D〉] and FA, which are the 2 most widely used DTI indices), the individual eigenvalues (λ1, λ2, and λ3) of the diffusion tensor were also used because they may provide additional information.13–14,25–28 Therefore, we analyzed in this study 5 DTI indices: FA, 〈D〉, λ1, λ2, and λ3.

Materials and Methods

Subjects

Fifteen healthy adult volunteers (aged 27–61 years; mean age, 38.8 years; 9 men and 6 women) participated in the study. None of participants had any history of neurologic disorder or brain injury. The study was approved by the institutional review board. Informed consent was obtained from all subjects after the nature of the study had been thoroughly described.

MR Imaging Protocols

All MR images were acquired on a GE Signa (Excite 11.0, GE Healthcare, Milwaukee, Wis) 1.5 T MR scanner with a standard quadrature head coil. In addition to conventional images (3D fast-spoiled gradient and fluid-attenuated inversion recovery) for whole brain anatomy, DTI images with a single-shot pulsed-gradient spin-echo echo-planar sequence in coronal orientation were obtained. For each subject, DTI images were acquired by using 3 protocols with different combinations of NDGD and NEX for each direction. The 3 DTI acquisitions were performed with 6, 21, and 31 noncollinear NDGD and were averaged (images were averaged on the fly) 10, 3, and 2 times for each image (ie, NDGD/NEX = 6/10, 21/3, 31/2). The 3 protocols resulted in almost the same total number of DW images for each section before signal intensity averaging (60, 63, and 62, respectively), and similar total scan time (9:36, 9:04, and 8:48 minutes and seconds, respectively). The order of the 3 protocols during acquisitions was randomized across the subjects to reduce bias in the data, in a single session for each subject. One reference (b = 0) image for each section was acquired for all 3 protocols with same NEX averages. DTI was acquired in an interleaved fashion; ie, 1 b = 0 image for every sections was acquired before all diffusion-encoded images in every repeat set. Other parameters for DTI were: repetition time/echo time = 8000/85 ms, matrix = 128 × 128, FOV = 24 cm, section thickness/gap = 3.8/0 mm, and b-factor = 1000 s/mm2, 28 sections with the center of corpus callosum (CC) as the middle of coverage.

Definitions of DTI Indices

From all diffusion-weighted images, the general diffusion tensor was first diagonalized, and the yielded scalar invariants of the tensor, including diffusion eigenvalues λ1, λ2, and λ3, were derived for each image pixel. λ1, λ2, and λ3 were used to calculate 〈D〉 and FA, which are defined as 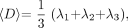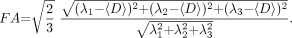Math Math 〈D〉, FA, λ1, λ2, and λ3 were used as DTI indices to compare the 3 protocols. All DTI indices were calculated and corresponding maps were created with the use of custom software.

Image Postprocessing

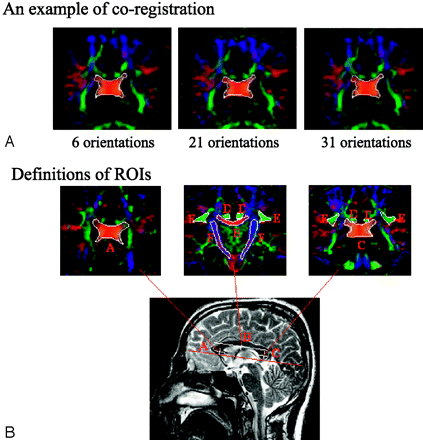
Before tensor calculation, images were corrected for motion artifact and eddy current distortion for each subject with the use of an algorithm proposed by Andersson and Skare29 that corrects interprotocol motion artifacts and eddy current artifacts simultaneously. Image coregistrations were performed among the 3 DTI datasets with the use of AIR 5.0 (http://bishopw.loni.ucla.edu/AIR5) to minimize the bias caused by subject motion during scanning. For each subject, images without diffusion weighting (b = 0) in 1 of the 3 protocol datasets were randomly selected as reference, and images (b = 0) from the other 2 protocols were coregistered to this reference. The generated transformation matrix was then applied to all DW images within same protocol. After coregistration, regions of interest (ROIs) were drawn manually on images from 1 protocol selected randomly, and these ROIs were then translated to the other 2 protocols for calculation of all 5 DTI indices. Figure 1A is an example of the coregistration results among the images of the 3 protocols, with ROI definition for the posterior portion of CC.

Fig 1.
Fig 1.

A, An example of coregistration across 3 protocols. Images on the left, middle, and right are obtained with the 6-NDGD, 21-NDGD, and 31-NDGD protocols, respectively. A region of interest (ROI) of the splenium of CC is initially drawn on only 1 image from 1 of the 3 protocols and then translated to the corresponding images from the other 2 protocols.

B, Spatial definition of ROIs: all ROIs are positioned relative to CC in the anterior (A, CCA), middle [B, CCM, cingulum (D), SLF (E), and IC (F)], and posterior [C, CCP, cingulum (D), and SLF (E)] locations.

ROI Selection

We selected 6 different ROIs, primarily encompassing white matter structures with considerably varying anisotropy. These ROIs, which are commonly used in many clinical DTI studies, were also well visible and distinguishable to be easily delineated in colored FA maps. The different protocols were compared for each of the following 6 white matter ROIs: callosal fibers, including anterior genu (CCA), middle body (CCM), and posterior splenium (CCP); association fibers, bilateral superior longitudinal fasciculus (SLF); limbic system fibers, bilateral cingulum (CIN); and projection fibers, internal capsule (IC).

ROIs were defined with respect to the CC; ie, the ROIs were positioned at 3 locations (Fig 1B, A, B, C): the center of genu of CC (for CCA), the center of CC (for CCM, middle CIN, middle SLF, and IC), and the center of splenium (for CCP, posterior CIN, and posterior SLF). Three adjacent sections were included for every ROI. The CIN and SLF were combined with bilateral ROIs in the middle and posterior locations, and the IC was combined with bilateral ROIs in the middle CC location. We used the Atlas of Human White Matter Anatomy30 as an additional tool for defining ROIs. Each individual ROI was manually delineated by using color-coded FA maps with average numbers of voxels of 748 for CCA, 410 for CCM, 1336 for CCP, 371 for CIN, 1002 for SLF, and 1275 for IC. An example of the tracing of ROIs is shown in Fig 1B. Manual delineation of the ROIs was performed independently by 2 of the authors, and no significant differences were found between their measurements. Voxels contaminated with CSF were eliminated with filters for FA < 0.01, and 〈D〉 1.70 × 10−3 mm2/s.

Data Analyses

Two levels of analyses were performed to test the effects of different NDGDs from 3 protocols.

ROI Level.

Mean values and their standard error of means (SEMs) for FA, 〈D〉, λ1, λ2, and λ3 from each ROI were separately analyzed in a 1-way repeated measures analysis of variance (ANOVA), with NDGD as a within-subject categoric variable. Greenhouse-Geisser adjustment31 for degrees of freedom was applied to the NDGD factor because of the inherent violation of the repeated measures assumption of sphericity. Where appropriate, post hoc analyses were conducted using the Tukey Honestly Significant Difference tests32 with a family-wise error rate of .05.

Voxel Level.

We evaluated the similarity among the 3 protocols with different NDGDs by comparing pair-wise correlation coefficients (r) for FA, 〈D〉, λ1, λ2, and λ3 values on a voxel-by-voxel basis for each ROI. For each DTI index and each ROI, we computed 3 correlation coefficients: r21–31 (between 21-NDGD and 31-NDGD protocols), r6–21 (between 6-NDGD and 21-NDGD protocols), and r6–31 (between 6-NDGD and 31-NDGD protocols). r6–21, r6–31, and r21–31 were compared in 1-way repeated measures ANOVA for all ROIs. Finally, we evaluated the correlation coefficients of FA as a function of mean anisotropy in the ROIs.

Results

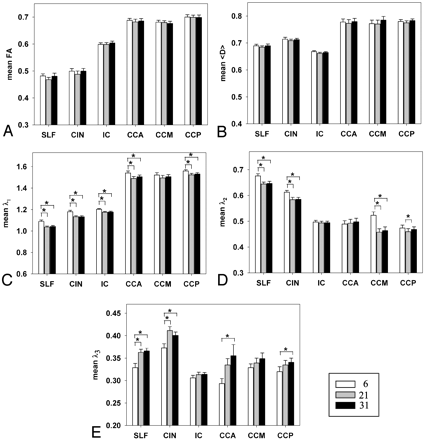
For ANOVA analysis at ROI level, the mean values of FA, 〈D〉, λ1, λ2, and λ3 for the 3 protocols are summarized in Fig 2 for all ROIs. Neither FA nor 〈D〉 showed significant differences among the 3 protocols (P > .05) (Fig 2A, -B). However, there were significant effects of NDGD on the 3 eigenvalues. Post hoc analyses showed that λ1 of the 6-NDGD protocol was higher than λ1 of the 21-NDGD and 31-NDGD protocols in 5 of 6 ROIs (Fig 2C): CCA, CCP, CIN, SLF, and IC (P < .002). λ2 of the 6-NDGD protocol was also higher than λ2 of the 21-NDGD and 31-NDGD protocols in 4 of 6 ROIs (Fig 2D): CCM, SLF, and CIN (P < .0001), but in CCP only between 6-NDGD and 21-NDGD protocols (P = .04). In contrast, λ3 of the 6 NDGD protocol was lower than those of the 21-NDGD and 31-NDGD protocols in 2 of 6 ROIs (Fig 2e): SLF and CIN (P < .0001), whereas in CCA and CCP, λ3 of the 6-NDGD was significantly lower than in 31-NDGD (P < .02). Analyses of SEMs in ROIs for FA, 〈D〉, λ1, λ2, and λ3 measures showed no significant differences for any of the DTI indices in any of the ROIs among the 3 protocols.

Fig 2.
Fig 2.

Mean value in 6 ROIs for the 3 protocols; A for FA, B for 〈D〉, C for λ1, D for λ2, and E for λ3. 〈D〉, λ1, λ2, and λ3 are measured in 10−3 mm2/s. White bars for 6-NDGD, gray bars for 21-NDGD, and black bars for 31-NDGD protocols. *, P < .05. Error bars are for 1 SEM.

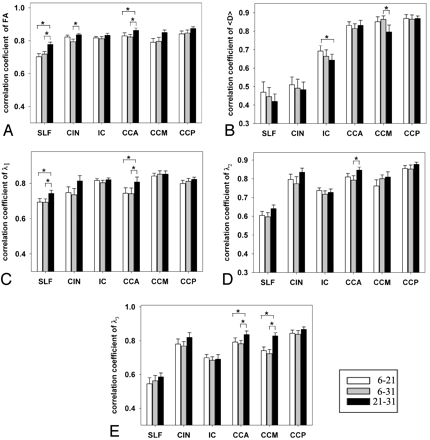
For ANOVA analyses at the voxel level, we used voxel as the random variable. Because of the large number of voxels, ANOVA analyses possessed such a power that even miniscule, empirically insignificant differences among the 3 protocols (eg, 1% change in FA), became significant. Thus, we evaluated the differences among the 3 protocols by correlating the DTI indices obtained at voxel level for each ROI. Figure 3 shows correlation coefficients across the 3 protocols for the 5 DTI indices in all ROIs. Overall, r21–31 was always higher than r6–21 and r6–31 in all ROIs for FA and λ1, in almost all ROIs for λ2 and λ3 (r21–31 was only lower than r6–21 in IC for λ2 and λ3), but not for 〈D〉. However, ANOVA and post hoc analyses showed significantly higher r21–31 than r6–21 and r6–31 for FA in CCA and SLF (P < .05) (Fig 3A), for λ1 in CCA and SLF (P < .05) (Fig 3C), and for λ3 in CCA and CCM (P < .03) (Fig 3E). Analyses also showed significantly higher r21–31 than r6–31 in CIN for FA and in CCA for λ2 (Fig 3D) (P < .03). However, for 〈D〉 r6–31 was higher than r21–31 in CCM and r6–21 was higher than r21–31 in IC (P < .03).

Fig 3.
Fig 3.

Correlation coefficient (r) in 6 ROIs between 2 of the 3 protocols. A for FA, B for 〈D〉, C for λ1, D for λ2, and E for λ3. White bars are for r6–21, gray bars for r6–31, and black bars for r21–31. *, P < .05. Error bars are for 1 SEM.

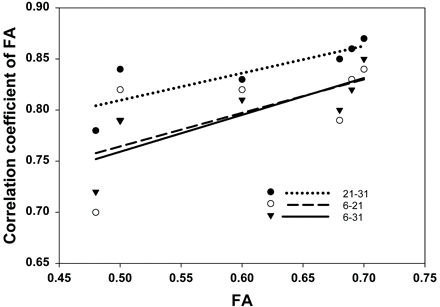
The relationship between correlation coefficients of FA and the mean anisotropy in different ROIs is illustrated in Fig 4. Linear fitting of r with FA revealed that there was a positive trend of r21–31, r6–21, and r6–31 with increasing anisotropy in ROIs. There was a significant linear relationship for r21–31 and for r6–31 (P < .05), but not for r6–21 (P > .05).

Fig 4.
Fig 4.

The linear fitting between correlation coefficient of FA versus FA value of different ROIs.

Discussion

Calculation of diffusion tensor D is based on apparent diffusion coefficient values from each diffusion-weighting direction. Both increasing NDGD and more averaging of DW images along each diffusion direction (ie, larger NEX) may improve estimation of D. So far, theoretic analysis and computer simulations19–24 have been used to investigate the effects of SNR in images and different NDGD on quantification of FA and 〈D〉. Our in vivo human brain study provided a real-world case test for these simulation and numeric studies. In our study, different combinations of NDGD and NEX are compared, with a similar total scanning time. For the protocol with larger NDGD, more DW images are acquired but with less averaging (ie, a lower SNR) for each DW image; for protocols with fewer NDGD, there are fewer DW images, but more averaging or a higher SNR for each DW image. First, we found that at the ROI level, FA and 〈D〉 showed no significant difference due to the number of diffusion gradient directions. Second, we found that at the voxel level, the 3 protocols did not provide consistent measures, but 21 and 31 diffusion gradient directions provided more similar measures of FA than the 6-direction protocol.

It is known that noise in DW images introduces errors in calculated diffusion tensor that propagates through diagonalization into final calculations of eigenvalues, FA, and diffusivity. It is also generally believed that the larger the NDGD, the lesser the error. Our ROI-based analysis, however, resulted in comparable values of FA and 〈D〉 for 3 levels of NDGD, suggesting that 6 or larger NDGDs will generate similar FA and 〈D〉. A simulation study23 found decreasing variation in estimates of FA and trace as the number of sampling directions increases, but the effect diminishes as SNR for images increases. Another study22 showed that the bias of mean FA values can be reduced more by increasing SNR than by increasing NDGD; with the SNR0 (SNR for b = 0 image) in the range of 10–100, the relationship between the FA and number of DW directions was independent. In our study the SNR0 was in the range of 27–60 (lowest for the 31-NDGD protocol with 2 averages of b = 0 images, and highest with the 6-NDGD protocol with 10 averages of b = 0 images). According to studies that have investigated the issue of effects of SNR on DTI,19,22,23,33,34 the SNRs used in the present study are in the range where noise variation will have minimal effects on these DTI indices such as FA and 〈D〉. With higher SNR, less variance is expected; however, acquisition time will be longer and this is generally beyond what is accepted for practical clinical use. The protocol parameters we used here were designed to get high SNR with a clinically acceptable acquisition time.

In contrast with the ROI analyses, our correlation analyses at the voxel level showed that r21-31 was higher than r6-21 and r6–31 for FA, suggesting that measurements with 21-NDGD are closer to 31-NDGD than to 6-NDGD protocols. Some previous simulation studies23,24 have shown that when the NDGD is larger, there is less uncertainty and error propagation. The work by Jones23 specifically suggests that at least 20 unique sampling orientations are necessary for a robust estimate of anisotropy. Our results are consistent with these conclusions suggesting that increasing NDGD beyond 21 has little effect on FA, and 21-NDGD is probably sufficient for in vivo human study of FA. However, for 〈D〉, the r21–31, r6–21, and r6–31 display random variations in different ROIs, which also probably suggests that NDGD less than 31 has not reached the stable measure for 〈D〉. This result also supports the view that at least 30 unique sampling orientations are required for a robust estimate of mean diffusivity.23

Increased correlations of FA between the 3 protocols with increase in anisotropy (Fig 4) indicate that the higher the anisotropy, the closer the similarity among protocols with different NDGDs. Furthermore, these findings suggest that DTI protocols are more reliable in FA estimations from ROIs with high anisotropy. This finding is again in accordance with the report23 showing that absolute uncertainty of FA decreases with the increase in anisotropy.

In our study, ROI-based analysis showed significant differences between 3 protocols for mean λ1, λ2, and λ3, but not for FA and 〈D〉. It is not clear at the moment whether this is because DTI eigenvalues are more sensitive than 〈D〉 or FA to biologic variations, or for some other reasons. These differences among eigenvalues may also be partly related to SNRs. A Monte Carlo simulation34 showed that the accuracy of the computed individual eigenvalues is more influenced by noise contamination than compound indices such as FA and 〈D〉. In the present study, it is likely that the SNRs were not high enough for λ1, λ2, and λ3 calculations, which resulted in detectable effects from NDGD, but were sufficiently high for FA and 〈D〉, leading to a minimal effect of NDGD. Intuitively, calculations of FA and 〈D〉 by combining λ1, λ2, and λ3 may cancel at least partially the variation of each eigenvalue among the 3 protocols. The results only show significant differences in mean λ1, λ2, and λ3 between the protocol with 6-NDGD and the other 2 protocols, but not between protocols with 21-NDGD and 31-NDGD. In addition, correlation analyses at the voxel level showed that r21–31 was higher than r6–21 and r6–31 for λ1, λ2, and λ3 in most ROIs. Following the reasoning from the simulation studies,23,24 these results may imply that increasing NDGD beyond 21 has little effect on λ1, λ2, and λ3. Because we did not use protocols with NDGD between 6 and 21, we cannot provide exact information about the lowest NDGD necessary for a robust estimate of eigenvalues.

Furthermore, it is necessary to address the effect of motion that might affect the outcome of in vivo studies such as ours. Calculation of reliable DTI indices requires combination of raw images from different acquisitions in sequential scanning, which in turn makes DTI susceptible for motion artifacts. In our study, before calculations of diffusion tensor elements, all non–diffusion-weighted images and all DW images in different directions were coregistered within and among the 3 protocols (ie, motion artifacts were corrected in both “interprotocol” and “intraprotocol” modes). This step minimized motion effects during scanning. However, motion contaminations among different acquisitions in the same gradient direction for averaging were not completely eliminated, because images were output after simple signal intensity algebraic averaging in a GE clinical scanner; therefore, motion artifacts were corrected after images were averaged. It is possible, therefore, that the motion effect is more prominent for the protocol with 6-NDGD than the protocols with 21-NDGD and 31-NDGD, because image coregistration was performed for every 10, 3, and 2 images, respectively, in each case. Future study should try to separate the raw data for individual acquisitions before averaging and perform coregistration for all non–diffusion-weighted images and all DW images in different directions for different acquisitions in 3 protocols. Cardiac gating may also be used to minimize pulsation effects, another variant of motion artifact.

There are usually limitations in the total number of images allowed in each series (on the GE scanner we used for this study, the limit was 1024 images). Larger NDGDs results in more images after average because in most scanners, images are averaged on the fly. Therefore, there is a trade-off between NDGDs and number of sections. Protocols with fewer NDGDs (such as 6) allow for more sections or repetitions, when the total number of images allowed is limited.

Finally, it should be emphasized that DTI measurements in general are very sensitive to even minor differences in hardware and software, acquisition parameters, and processing details. The conclusions from this study with a limited number of acquisitions protocols on a single scanner should therefore be taken with precaution. More data may be needed before these results can be generalized. It is hard or impossible to obtain a “gold standard” for human study. Without such a standard, it is impossible to completely evaluate reliability or consistency of acquisition protocols. More sophisticated and probably more exhaustive studies may be needed to obtain ultimate conclusions.

Conclusion

In summary, this study suggested that the 3 protocols with 6, 21, and 31 NDGDs generate significant differences for ROI-based λ1, λ2, and λ3 measurements but not for FA and 〈D〉 measurements. Voxel-based analyses, on the other hand, showed significant differences of NDGDs for all DTI indices. Therefore, it is likely that for applications in which only mean values of FA and 〈D〉 measurements within ROIs are needed and detailed voxel-based effects can be ignored, the NDGDs employed do not make much difference as long as the SNR is above a certain minimum level, and a protocol with 6-NDGD is sufficient. For applications in which λ1, λ2, and λ3 measures within ROIs are needed, protocols with more than 21 NDGDs are necessary for estimation of these eigenvalues. For applications in which voxel-based information is desired, such as in longitudinal studies of disease progress or monitoring of treatment effects, a protocol with at least 21 NDGD should be used for estimation of FA, λ1, λ2, and λ3, and a protocol with at least 31 NDGD should be used for estimation of 〈D〉. Our results showed that when similar acquisition time is maintained, NDGD has greater effect than NEX at NDGD lower than 21 for eigenvalues analysis and voxel-based FA analysis and at NDGD lower than 31 for voxel-based diffusivity analysis. Clinical DTI protocols should be better designed to balance the trade-offs between NDGD and NEX, together with shorter scan time and more sections. In addition, for applications with different ROIs, regions with lower anisotropy may need protocols with larger NDGDs for reliable FA estimation. Because the study used a limited number of acquisitions protocols on a single scanner, precaution should be taken in generalizing the above conclusions.

Acknowledgments

We appreciate Robert Ambrosini’s help in coregistration of images.

Footnotes

  • This work was supported by National Institutes of Health grant NS32024, the Schmitt Foundation, and the American Alzheimer’s Association.

  • This work was presented in part at the 90th Scientific Assembly and Annual Meeting of the Radiological Society of North America as an oral Scientific Presentation; Nov 28–Dec 3, 2004; Chicago, Ill.

References

  1. ↵
    Chepuri NB, Yen YF, Burdette JH, et al. Diffusion anisotropy in the corpus callosum. AJNR Am J Neuroradiol 2002;23:803–08
    Abstract/FREE Full Text
  2. Takahashi S, Yonezawa H, Takahashi J, et al. Selective reduction of diffusion anisotropy in white matter of Alzheimer disease brains measured by 3.0 Tesla magnetic resonance imaging. Neurosci Lett 2002;332:45–48
    CrossRefPubMed
  3. ↵
    Fellgiebel A, Wille P, Muller MJ, et al. Ultrastructural hippocampal and white matter alterations in mild cognitive impairment: a diffusion tensor imaging study. Dement Geriatr Cogn Disord 2004;18:101–08
    CrossRefPubMed
  4. ↵
    Zhong J, Ni H, Zhu T, et al. MR diffusion tensor imaging (DTI) and neuropsychological testing for neuronal connectivity in Alzheimer’s disease (AD) patients. Proceedings of SPIE: Medical Imaging 2004—Physiology, Function, and Structure from Medical Images 2004;5369:238–49
  5. ↵
    Coombs BD, Best A, Brown MS, et al. Multiple sclerosis pathology in the normal and abnormal appearing white matter of the corpus callosum by diffusion tensor imaging. Mult Scler 2004;10:392–97
    Abstract/FREE Full Text
  6. Kealey SM, Kim Y, Provenzale JM. Redefinition of multiple sclerosis plaque size using diffusion tensor MRI. AJR Am J Roentgenol 2004;183:497–503
    PubMed
  7. Cassol E, Ranjeva JP, Ibarrola D, et al. Diffusion tensor imaging in multiple sclerosis: a tool for monitoring changes in normal-appearing white matter. Mult Scler 2004;10:188–96
    Abstract/FREE Full Text
  8. Ciccarelli O, Werring DJ, Barker GJ, et al. A study of the mechanisms of normal-appearing white matter damage in multiple sclerosis using diffusion tensor imaging—evidence of Wallerian degeneration. J Neurol 2003;250:287–92
    CrossRefPubMed
  9. Bozzali M, Cercignani M, Sormani MP, et al. Quantification of brain gray matter damage in different MS phenotypes by use of diffusion tensor MR imaging. AJNR Am J Neuroradiol 2002;23:985–88
    Abstract/FREE Full Text
  10. Guo AC, MacFall JR, Provenzale JM. Multiple sclerosis: diffusion tensor MR imaging for evaluation of normal-appearing white matter. Radiology 2002;222:729–36
    PubMed
  11. Guo AC, Jewells VL, Provenzale JM. Analysis of normal-appearing white matter in multiple sclerosis: comparison of diffusion tensor MR imaging and magnetization transfer imaging. AJNR Am J Neuroradiol 2001;22:1893–900
    Abstract/FREE Full Text
  12. Cercignani M, Inglese M, Pagani E, et al. Mean diffusivity and fractional anisotropy histograms of patients with multiple sclerosis. AJNR Am J Neuroradiol 2001;22:952–58
    Abstract/FREE Full Text
  13. ↵
    Oh J, Henry RG, Genain C, et al. Mechanisms of normal appearing corpus callosum injury related to pericallosal T1 lesions in multiple sclerosis using directional diffusion tensor and 1H MRS imaging. J Neurol Neurosurg Psychiatry 2004;75:1281–86
    Abstract/FREE Full Text
  14. ↵
    Henry RG, Oh J, Nelson SJ, et al. Directional diffusion in relapsing-remitting multiple sclerosis: a possible in vivo signature of Wallerian degeneration. J Magn Reson Imaging 2003;18:420–26
    CrossRefPubMed
  15. ↵
    Clark CA, Hedehus M, Moseley ME. Diffusion time dependence of the apparent diffusion tensor in healthy human brain and white matter disease. Magn Reson Med 2001;45:1126–29
    CrossRefPubMed
  16. ↵
    Ragin AB, Storey P, Cohen BA, et al. Whole brain diffusion tensor imaging in HIV-associated cognitive impairment. AJNR Am J Neuroradiol 2004;25:195–200
    Abstract/FREE Full Text
  17. Pomara N, Crandall DT, Choi SJ, et al. White matter abnormalities in HIV-1 infection: a diffusion tensor imaging study. Psychiatry Res 2001;106:15–24
    CrossRefPubMed
  18. ↵
    Filippi CG, Ulug AM, Ryan E, et al. Diffusion tensor imaging of patients with HIV and normal-appearing white matter on MR images of the brain. AJNR Am J Neuroradiol 2001;22:277–83
    Abstract/FREE Full Text
  19. ↵
    Papadakis NG, Xing D, Houston GC, et al. A study of rotational invariant and symmetric indices of diffusion anisotropy. Magn Reson Imaging 1999;17:881–92
    CrossRefPubMed
  20. ↵
    Skare S, Hedehus M, Moseley ME, et al. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. J Magn Reson 2000;147:340–52
    CrossRefPubMed
  21. ↵
    Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. J Magn Reson Imaging 2001;13:769–80
    CrossRefPubMed
  22. ↵
    Papadakis NG, Murrills CD, Hall LD, et al. Minimal gradient encoding for robust estimation of diffusion anisotropy. Magn Reson Imaging 2000;18:671–79
    CrossRefPubMed
  23. ↵
    Jones DK. The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: a Monte Carlo study. Magn Reson Med 2004;51:807–15
    CrossRefPubMed
  24. ↵
    Poonawalla AH, Zhou XJ. Analytical error propagation in diffusion anisotropy calculations. J Magn Reson Imaging 2004;19:489–98
    CrossRefPubMed
  25. ↵
    Song SK, Sun SW, Ramsbottom MJ, et al. Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. NeuroImaging 2002;17:1429–36
    CrossRef
  26. Peng SS, Tseng WY, Chien YH, et al. Diffusion tensor images in children with early-treated, chronic, malignant phenylketonuric: correlation with intelligence assessment. AJNR Am J Neuroradiol 2004;25:1569–74
    Abstract/FREE Full Text
  27. Thomalla G, Glauche V, Koch MA, et al. Diffusion tensor imaging detects early Wallerian degeneration of the pyramidal tract after ischemic stroke. Neuroimage 2004;22:1767–74
    CrossRefPubMed
  28. ↵
    Peng SS, Lee WT, Wang YH, et al. Cerebral diffusion tensor images in children with tuberous sclerosis: a preliminary report. Pediatr Radiol 2004;34:387–92
    CrossRefPubMed
  29. ↵
    Andersson JH, Skare S. A model-based method for retrospective correction of geometric distortions in diffusion-weighted EPI. Neuroimage 2002;16:177–99
    CrossRefPubMed
  30. ↵
    Wakana S, Jiang H, Nagae-Poetscher LM, et al. Fiber tract-based atlas of human white matter anatomy. Radiology 2004;230:77–87
    CrossRefPubMed
  31. ↵
    Greenhouse SW, Geisser S. On methods in the analysis of profile data. Psyhometrika 1959;24:95–112
    CrossRef
  32. ↵
    Keselman HJ, Rogan JC. The Tukey multiple comparison test: 1953–1976. Psychological Bulletin 1977;84:1050–56
    CrossRef
  33. ↵
    Anderson AW. Theoretical analysis of the effects of noise on diffusion tensor imaging. Magn Reson Med 2001;46:1174–88
    CrossRefPubMed
  34. ↵
    Pierpaoli C, Basser PJ. Toward a quantitative assessment of diffusion anisotropy. Magn Reson Med 1996;36:893–906
    CrossRefPubMed
  • Received July 19, 2005.
  • Accepted after revision December 16, 2005.
View Abstract
Back to top

In this issue

Advertisement
Print
Download PDF
Email Article
Citation Tools
Effects of Number of Diffusion Gradient Directions on Derived Diffusion Tensor Imaging Indices in Human Brain
H. Ni, V. Kavcic, T. Zhu, S. Ekholm, J. Zhong
American Journal of Neuroradiology Sep 2006, 27 (8) 1776-1781;
del.icio.us logo Twitter logo Facebook logo Mendeley logo

Jump to section

Advertisement