Abstract
BACKGROUND AND PURPOSE: Recent high-resolution computational fluid dynamics studies have uncovered the presence of laminar flow instabilities and possible transitional or turbulent flow in some intracranial aneurysms. The purpose of this study was to elucidate requirements for computational fluid dynamics to detect these complex flows, and, in particular, to discriminate the impact of solver numerics versus mesh and time-step resolution.
MATERIALS AND METHODS: We focused on 3 MCA aneurysms, exemplifying highly unstable, mildly unstable, or stable flow phenotypes, respectively. For each, the number of mesh elements was varied by 320× and the number of time-steps by 25×. Computational fluid dynamics simulations were performed by using an optimized second-order, minimally dissipative solver, and a more typical first-order, stabilized solver.
RESULTS: With the optimized solver and settings, qualitative differences in flow and wall shear stress patterns were negligible for models down to ∼800,000 tetrahedra and ∼5000 time-steps per cardiac cycle and could be solved within clinically acceptable timeframes. At the same model resolutions, however, the stabilized solver had poorer accuracy and completely suppressed flow instabilities for the 2 unstable flow cases. These findings were verified by using the popular commercial computational fluid dynamics solver, Fluent.
CONCLUSIONS: Solver numerics must be considered at least as important as mesh and time-step resolution in determining the quality of aneurysm computational fluid dynamics simulations. Proper computational fluid dynamics verification studies, and not just superficial grid refinements, are therefore required to avoid overlooking potentially clinically and biologically relevant flow features.
ABBREVIATIONS:
- CFD
- computational fluid dynamics
- HR
- high-resolution
- k
- thousand
- M
- million
- MWSS
- maximum wall shear stress
- NR
- normal-resolution
- OSI
- oscillatory shear index
- WSS
- wall shear stress
Image-based computational fluid dynamics (CFD) has become an essential tool for investigating intracranial aneurysm hemodynamics and its possible role in aneurysm initiation, growth, rupture, and treatment outcome. Notably, retrospective studies have demonstrated associations between low or high wall shear stress (WSS) and rupture status, with the goal of improving rupture-risk assessment. Although attempts have been made to unify these opposing hemodynamic factors,1 skepticism about CFD remains, owing to the wide variety of proposed hemodynamic factors and definitions,2 the various modeling assumptions and uncertainties,3 and the focus on lumen versus the wall.4 Nevertheless, medical imaging vendors are actively seeking to deploy CFD solvers on their scanner platforms.5
A recent study has highlighted a largely unacknowledged source of uncertainty: the strong dependence of the simulations on the CFD solution strategy.6 In that study, a so-called high-resolution (HR) strategy, combining a high-fidelity CFD solver with fine mesh and time-step resolutions, uncovered high-frequency flow instabilities in 4/8 MCA bifurcation aneurysm cases. On the other hand, these instabilities were completely suppressed by a so-called normal-resolution (NR) strategy, combining a solver and resolutions more representative of the aneurysm CFD literature.
In not separating the impact of solver numerics versus model resolution, the aforementioned study may have left the impression that highly refined CFD meshes and time-steps, and thus clinically unsupportable computation times, might be required to predict complex aneurysmal flow features. For the present study, we hypothesized that solver numerics (by which we mean the solver discretization scheme and settings) are at least as important as mesh and time-step resolution in determining the fidelity of aneurysm CFD solutions. To test this hypothesis and to determine whether instabilities can be detected, if not necessarily resolved, at lower CFD model resolutions (and hence more clinically supportable time scales), the present study varied, independently, the CFD solver numerics, mesh resolution, and time-stepping to identify their relative impacts on qualitative and quantitative hemodynamics of intracranial aneurysms.
Materials and Methods
The study focused on 3 different anatomically plausible MCA aneurysms (Fig 1), previously shown to exhibit, and specifically chosen to exemplify, highly unstable (case 16), mildly unstable (case 9), and stable (case 8) flows, respectively.6,7 Pulsatile simulations were performed by using an ICA flow waveform shape derived from older adults8 and damped by 30% to account for its transit from the cervical-to-cavernous segments.9 We applied a cross-sectional time-averaged velocity of 0.37 m/s,6 resulting in cycle-averaged flow rates of 1.11, 1.93, and 2.12 mL/s for cases 8, 9, and 16, respectively. Fully developed Womersley velocity profiles were applied at the inlet, and zero pressure was specified at the outlets. Three cardiac cycles were simulated to wash out initial transients. Blood viscosity and attenuation were assumed to be 0.035 mPa-s and 1 g/cm3, respectively.
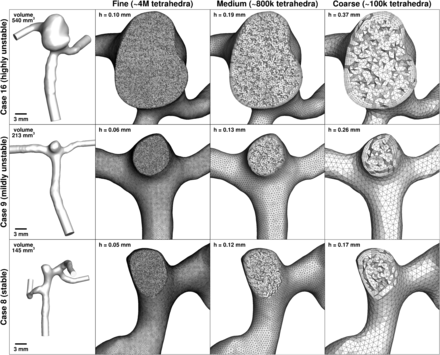
Fine, medium, and coarse meshes for each of the 3 MCA aneurysm cases. Nominal tetrahedral side length in the sac (h) is indicated at the top left of each mesh panel. The leftmost column shows the full lumen models, to the same scale, and with model volumes indicated. The ultrafine (32M) meshes are too attenuated to show, having effective tetrahedral side lengths of half those of the fine (4M) meshes.
As summarized in the Table, various permutations of spatial (mesh) resolution, temporal (time-step) resolution, and CFD solver were considered for each of the 3 cases. First, to isolate the effects of spatial resolution, we performed simulations by using the HR solver with fine time-stepping for 4 different meshes, generated by using the Vascular Modeling ToolKit (http://www.vmtk.org). The reference (ultrafine) meshes comprised ∼4 million (4M) second-order tetrahedra, roughly equivalent to ∼32M linear tetrahedra. The fine meshes comprised the same ∼4M elements, but now by using linear tetrahedra. Medium and coarse meshes comprised ∼800,000 (800k) and ∼100,000 (100k) linear tetrahedra, respectively. All used 4 boundary layer elements, with the total boundary layer thickness set to the nominal tetrahedral element side length. Per Fig 1, the 320-fold difference in the number of elements corresponded to nearly an order of magnitude variation in tetrahedron side length (ie, spatial resolution).
Model identifiers and CPU times for the various permutations of spatial resolution, temporal resolution, and solver
For the above studies, a reference (fine) temporal resolution was set to 35,000 (35k) time-steps per cardiac cycle, to satisfy the well-known Courant-Friedrich-Lewy stability condition for the ultrafine meshes. Per the Table, to independently isolate the effects of temporal resolution, the number of time-steps/cycle was reduced to 5600 (5.6k) and then 1400 (1.4k). These simulations, spanning a 25-fold difference in temporal resolution, were performed by using the medium (800k) meshes, after observing that they had adequate spatial resolution. To test the limits of solution accuracy, we also performed a coarse (100k) mesh and time-step (1.4k) simulation for each case.
The above-described simulations used a second-order-accurate, minimally dissipative, and energy-preserving CFD solver10 (described previously as the HR solver,6 and available as an open-source code at https://github.com/mikaem/Oasis). To independently isolate the effect of the solver, per the Table, we performed the same simulations described for the temporal resolution subanalysis by using the NR solver,6 which is stabilized and first-order-accurate in space and time to mimic the default settings in commercial solvers like Fluent (ANSYS, Canonsburg, Pennsylvania) and Star-CD (CD-adapco, Melville, New York).
The impact of resolution and solver was evaluated qualitatively via volumetric maps of velocity magnitude, surface maps of cycle-averaged WSS magnitude and oscillatory shear index (OSI), and traces of velocity and WSS magnitude from selected probe points. For quantitative evaluations, we computed the following nominal predictors of rupture status for each combination of case and model6: dome-averaged WSS and dome-maximum WSS (MWSS), both normalized to the parent artery WSS, and dome-averaged OSI.
Results
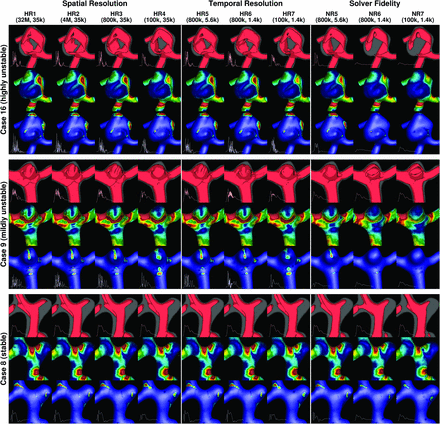
Qualitative results are summarized in the comprehensive Fig 2. If one focuses first on spatial (mesh) resolution effects, it can be seen that from the equivalent of 32M elements down to 800k elements (HR1, HR2, and HR3), there were negligible differences in velocity, WSS, and OSI levels and distributions for all cases. Notably, for unstable cases 16 and 9, all models appeared to capture similar flow instabilities, per the inset velocity and WSS traces. Further coarsening of the meshes to 100k elements (HR4) introduced an evident reduction in WSS levels, as well as a dampening (but not complete suppression) of velocity and WSS instabilities for cases 16 and 9. On the basis of the 320-fold difference in mesh sizes, we concluded that mesh size is relatively insensitive for the commonly reported hemodynamic variables and thus alone cannot inform whether a CFD simulation is adequate.
Qualitative impact of spatial resolution, temporal resolution, and solver fidelity on velocity and wall shear stress distributions. For each of the 3 aneurysm cases, the top row shows isosurfaces (0.3 m/s) of early diastolic velocity magnitude, the middle row shows time-averaged WSS magnitude (scale: 0–15 Pa), and the bottom row shows the oscillatory shear index (scale: 0.0–0.3). The inset into each velocity isosurface panel is a velocity-versus-time trace, from a selected point within the sac. Similarly, the inset into each OSI panel is a WSS magnitude-versus-time trace, from a point on the sac experiencing relatively high OSI.
With the 800k meshes as a basis for the temporal (time-step) resolution investigation, negligible effects were seen in going from 35k to 5.6k steps/cycle (ie, HR3 versus HR5). Minor differences were evident with a further reduction to 1.4k steps/cycle (HR6), suggesting that a temporal resolution somewhere between these 2 values would be sufficient. This dramatic reduction in the number of time-steps had a similarly minor effect for the 100k meshes (HR4 versus HR7). Some differences were evident for the velocity traces for the 2 unstable flow cases (16 and 9), but even the coarsest models (HR7) were still able to detect, if not necessarily resolve, the flow instabilities.
On the other hand, simulations performed by using the normal-resolution solver (NR5–7 versus HR5–7) appeared to artificially suppress all flow instabilities. WSS maps were comparable with those of the corresponding HR models, but OSI was highly underestimated by the NR solver at 1.4k steps/cycle. This was improved by increasing the number of time-steps to 5.6k but still with an evident suppression of flow instabilities per the velocity and WSS traces. On the basis of the 25-fold difference in time-step size, we concluded that the number of time-steps is only moderately important, as long as the number of time-steps is >5000 per cycle.
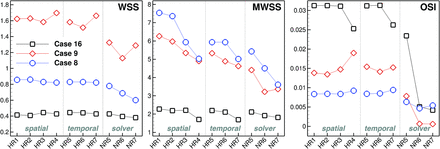
The quantitative impact on proposed scalar metrics of rupture status is shown in Fig 3. In particular, normalized, dome-averaged (time-averaged) WSS was relatively stable with mesh and temporal resolution by using our HR solver: Errors relative to the highest resolution (HR1) models were always <10%. For MWSS, there was a more evident reduction in values with each mesh coarsening, and at the coarsest resolutions with the HR solver, the rank ordering of cases by MWSS was altered. Especially for cases 8 and 9, MWSS values were evidently less accurate for the NR-versus-HR solver. For the HR solver, dome-averaged OSI was relatively unaffected down to the 800k meshes and 5.6k steps/cycle. Larger errors were evident at the coarser resolutions; however, the rank ordering by OSI was unaffected. The same could not be said for the NR solver, with almost complete suppression of OSI for the unstable cases 16 and 9, also affecting the rank ordering. Finally, even with an 8-fold increase in the number of elements (eg, NR6 versus NR7), the NR solutions were still far from the converged (HR) solutions, at least for the unstable flow cases.
The quantitative impact of spatial resolution, temporal resolution, and solver fidelity on various reduced hemodynamic indices, as indicated at the top right corner of each plot.
Discussion
We have demonstrated that CFD solver numerics had a more profound impact on commonly computed hemodynamic indices than the number of time-steps and, perhaps most surprising, mesh resolution. As discussed below, the importance of solver numerics was expected a priori; however, we were pleasantly surprised by the coarseness and hence speed with which an HR-type solver could achieve high-quality results relative to the reference solutions. As also discussed below, these findings have implications for the utility of CFD in a clinical setting and for basic research into aneurysm mechanobiology.
Implications for Clinical Timeframes
The clearest impact of the current results is that irrespective of flow phenotype, accurate hemodynamic indices can be obtained within clinically supportable timeframes provided a HR-type CFD solver is used. Per the Table and Fig 3, accurate solutions could be achieved by the HR solver on a standard desktop computer in ∼3 hours/cycle or ∼10 hours for a complete simulation. Furthermore, by showing that the coarse resolution simulations could at least detect the presence of flow instabilities, we can conclude that <1 hour of simulation time would be sufficient to assess the need for further refinement, of course provided a high-fidelity solver is used.
A corollary of this is that the absence of flow instabilities in an NR-type simulation cannot be taken as prima facie evidence of stable aneurysm flow. As such, and as our results suggest, NR-type simulations might, ironically, require finer resolutions and hence longer run times than what is typically reported. This supposition is not to imply that detection of flow instabilities is a sine qua non for the investigation of aneurysm hemodynamics, but rather that their absence in the aneurysm CFD literature may be the result of numeric artifacts that are inadvertently serving to suppress plausible avenues of investigation. Nor is it intended to impugn the findings of aneurysm CFD “trials,” because we have previously shown that NR-type simulations can consistently rank cases by using reduced-order hemodynamic indices (eg, time- and dome-averaged WSS) and, hence, nominally, rupture status, albeit with a 50% underestimation of WSS magnitudes.6 As noted in the next section, however, results from NR solvers may well be misleading regarding the pathophysiology of aneurysm initiation and rupture.
Implications for Aneurysm Mechanobiology
Just like morphologic discriminants, reduced hemodynamic indices are only an echo of some putative mechanistic link between the hemodynamic stresses and the response of the wall. To elucidate those mechanobiologic links, one may need a thorough understanding of the spatiotemporal scales of the flow and WSS, which requires HR-type simulations. For example, by suppressing flow instabilities, NR-type simulations cannot easily explain the prevalence of aneurysm bruits,11,12 which are widely thought to be driven by high-frequency flow instabilities, whether laminar or turbulent. Furthermore, even though both NR5 and HR5 simulations showed comparable OSI distributions in Fig 2, the behavior behind them is different: For HR5, high OSI is due to high-frequency WSS instabilities, whereas for NR5, it is due to more sluggish WSS oscillations. The latter is characteristic of the type of flow for which OSI was originally developed, whereas is it known that different stimuli can give rise to the same OSI value.13 On the basis of the turbulent-like flows from the HR simulations, it thus seems likely that any correlations between rupture status and high OSI from NR-type studies do not necessarily reflect the mechanobiologic causation.
Although it remains to be proved, it is plausible that the dynamic WSS stimuli elicited by the HR-type simulations could be of importance for understanding the mechanobiology of aneurysm growth and rupture. Focus in aneurysm research has been on spatial WSS gradients,14 whereas temporal WSS gradients, shown to be of importance to mechanotransduction and gene expression,15 have received less attention, probably because prevalent NR-type simulations are unable to detect them. For example, Davies et al16 exposed endothelial cells in vitro to turbulent flows (ie, WSS stimuli phenotypically similar to what we see in some of the unstable flow cases) and showed that turbulence led to a lack of endothelial cell orientation and cell depletion and loss even for low-intensity disturbances. Fry17 investigated similar effects in vivo, and after just an hour of exposure to turbulent flows, reported endothelial cell swelling, deformation, and disintegration downstream of the plug. In short, it seems as though temporal WSS gradients may also be of importance.
Relationship to Previous Work
As alluded to by Ventikos,18 our findings would likely have been anticipated by experienced CFD users following verification guidelines laid out by engineering journals nearly 30 years ago. In 1986, the ASME Journal of Fluids Engineering emphasized in their editorial policy that “a single calculation of a fixed grid is not acceptable.”19 This journal has also said, “It has been demonstrated many times that for first-order methods, the effect of numeric diffusion on the solution accuracy is devastating,”20 consistent with what we have shown in the current study. However, a cursory inspection of articles published in the American Journal of Neuroradiology and other clinical (and indeed biomedical engineering) research journals reveals that accuracy or mesh and time-step refinement results are rarely or only superficially reported. We are aware of only 1 thorough presentation, by Hodis et al,21 who carried out an extensive mesh refinement study by using the popular commercial CFD solver, Fluent. Meshes ranged from a high of nearly 7000 nodes/mm3 to a low around 100 nodes/mm3.
Our study spanned a wider range, with ultrafine meshes comprising 8000–30,000 nodes/mm3 to coarse meshes with 30–100 nodes/mm3, and allowed investigation of the isolated effects of spatial and temporal resolution errors alone, in which the most resolved model was effectively 8000 (ie, 320 × 25) times finer than the coarsest one. Hodis et al21 also focused on a technically detailed convergence analysis of the peak systolic velocity vector field and its error norms, which, while salient, provided little context for the qualitative differences in the overall flow and WSS fields and/or derived scalar indices of potential clinical interest. Nevertheless, we arrived at similar conclusions to those of Hodis et al, namely that refined meshes are required, particularly if point values are desired. We disagree, however, with their assertion that “each patient-specific model require[s] its own grid convergence,” because this is laborious and not practicable in a clinical setting.
Our findings could also be anticipated from the results of a recent international CFD Challenge.22 There, peak systolic flow instabilities in a giant ICA aneurysm were predicted by only a handful of the 25 participating groups. Most of the contributed solutions (most by using commercial CFD solvers, predominantly Fluent) reported laminar flows with stable peak systolic flow patterns and with aneurysm jet inflow velocities damped to varying degrees. One of the conclusions was that at least 5000 time-steps/cycle appeared to be a necessary, albeit not a sufficient, condition for detecting flow instabilities. Our present findings would seem to suggest that even 1000 time-steps/cycle—the median of that used by the various CFD Challenge participants—are insufficient to resolve the dynamics of unstable aneurysm flows, even with a minimally dissipative, second-order-accurate CFD solver.
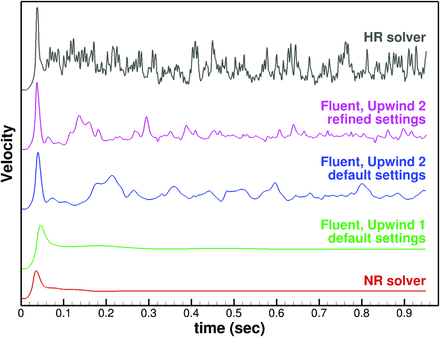
To see whether our findings could be extrapolated to a commercial solver, we performed transient steady flow simulations (to remove the confounding effects of pulsatility) for the most unstable flow, case 16, by using Fluent (Version 14; ANSYS). Steady inflow velocity was set to 0.5 m/s, corresponding to peak systolic conditions at the MCA.6 Simulations were performed for the 800k mesh and 1.4k time-steps, by using first-order upwinding (Fluent's default prior to 2012) and second-order upwinding (the current Fluent default), both with default solver settings (semi-implicit method for the pressure-linked equation method, first-order implicit time-stepping, “standard” pressure, 20 iterations/time-step, single precision, 10−3 convergence criterion). For second-order upwinding, the default settings were then refined (the PISO [pressure implicit with splitting of operator] method, second-order implicit time-stepping, second-order pressure, 50 iterations/time-step, double precision, 10−5 convergence criterion). The results, shown in Fig 4, indicate a strong sensitivity of velocity dynamics to upwind order and solver settings, independent of the solver itself. For example, the first-order upwinding of Fluent performed in a manner similar to that of our NR solver, both serving to damp any flow instabilities. The second-order upwinding of Fluent detected some flow instabilities, the frequency of which was clearly increased by expert refining of the default solver settings. These results are, therefore, approaching a solution that is referred to as minimally dissipative and energy-preserving.23
Impact of the progressively refined CFD solver and settings on transient simulation of steady flow for case 16, with 800k mesh and 1.4k time-steps.
It is worth noting that, for these expertly refined settings, we had to adjust both the number of iterations and the convergence tolerance to reach the desired convergence level, a subtlety that might be lost on a non-expert user. Nevertheless, not being perfectly fluent in Fluent, we could not get it to match the higher frequency and amplitude fluctuations evident from our HR solver. This inability to match our results to those of Fluent is not to imply that our finite-element-based HR solver is superior to Fluent and/or the finite volume method on which it is based. Rather, it highlights the importance of understanding well the capabilities of a CFD solver and its limitations to ensure reliable results.
Potential Limitations
We assumed rigid walls, Newtonian fluid, fully developed (laminar) inflow velocities, and generalized flow rates. These are commonly accepted assumptions, and their effects are now well-documented to be of relatively minor importance, at least for NR-type simulations. Moreover, our observed impact of solver settings on hemodynamic variables was, if anything, more pronounced than the previously reported impacts of the above-noted assumptions. Relevant limitations of the current study were the following: 1) It is unclear whether blood can still be modeled as a continuum for turbulent-like unstable flows.24 2) The assumption of fully developed laminar inflow may be questioned in light of recent evidence that the carotid siphon may have flow instabilities propagating into the MCA.25 3) Our study considered only 3 cases from a particular site (MCA), albeit chosen to exemplify a range of aneurysm flow phenotypes. 4) It remains unclear what is necessary to elucidate the mechanobiology or resolve instantaneous quantities. Finally, caution must be exercised in translating too literally the numbers of elements and time-steps that were sufficient for our purposes, for 2 main reasons: First, they obviously depend on the size of the aneurysm, the extent of the domain, and the dynamics of the imposed flow rates. Second, as we have clearly demonstrated here, they depend critically on the choice of CFD solver and its settings. Thus, we must emphasize that the recommended mesh and time-step sizes hold only for our HR solver—each user must perform their own verification studies.
Conclusions
We have shown that a robust and minimally dissipative CFD solver can tolerate surprisingly coarse resolutions, whereas solvers using low-order and/or stabilization schemes may, ironically, require much higher resolutions to detect, let alone properly resolve, complex flow in a potentially nonnegligible number of aneurysm cases. It is therefore essential that groups perform proper verification studies, per the recommendations of technical journals and, ideally, with the help of experts in CFD theory and practice, to arrive at solver settings and mesh/time-step resolutions that can be applied uncritically to any given case. This process is much in the same way that medical physicists play a critical role in setting clinical imaging protocols. If CFD is, ultimately, to operate as a putative medical imaging tool, it must have established local protocols that too are set by expert users by using rigorous calibration (ie, verification) methodologies.
Acknowledgments
The authors thank Maxwell Julian (University of Toronto), Peter Coppin (OCAD University), and Side Effects Software for their help in generating the data-driven, illustration-inspired velocity visualizations in Fig 2.
Footnotes
This work was supported by a Heart and Stroke Foundation of Canada grant (G-13-0001830) to D.A.S. Computations were performed on the General Purpose Cluster at the SciNet High Performance Computing Consortium. SciNet is funded by the Canada Foundation for Innovation under the auspices of Compute Canada; the Government of Ontario; Ontario Research Fund–Research Excellence; and the University of Toronto. D.A.S. also acknowledges the support of Mid-Career Investigator salary award from the Heart and Stroke Foundation.
Paper previously presented in part at: International Symposium on Biomechanics in Vascular Biology and Cardiovascular Disease, April 28–29, 2014, Montreal, Canada; the Interdisciplinary Cerebrovascular Symposium, June 2–4, 2014, Zurich, Switzerland; and the World Congress of Biomechanics, July 6–11, 2014, Boston, Massachusetts.
REFERENCES
- Received September 4, 2014.
- Accepted after revision November 19, 2014.
- © 2015 by American Journal of Neuroradiology
Jump to section
Related Articles
Cited By...
- Tube2FEM: a general-purpose highly-automated pipeline for flow related processes in (embedded) tubular objects
- Torrents of torment: turbulence as a mechanism of pulsatile tinnitus secondary to venous stenosis revealed by high-fidelity computational fluid dynamics
- 4D-CT angiography versus 3D-rotational angiography as the imaging modality for computational fluid dynamics of cerebral aneurysms
- Better Than Nothing: A Rational Approach for Minimizing the Impact of Outflow Strategy on Cerebrovascular Simulations