Abstract
BACKGROUND AND PURPOSE: We present a relatively simple approach that physicians can use to reconstruct cerebral vessels as 3D numerical grids or computational replicas. The method accurately duplicates their geometry to provide computer simulations of their blood flow.
METHODS: Initial images were obtained by using any medical imaging technique, such as MR angiography, CT angiography, or 3D digital subtraction angiography. The data were collected in DICOM format and converted by a DICOM reader into a 3D gray-scale raster image. The image was then processed by using commercial visualization and mesh generation software, which allowed extraction of the luminal surface of the blood vessel (by using the isosurfacing technique). The subsequent final output was an unstructured tetrahedral grid that can be directly used for detailed analysis of cerebral vascular geometry for patient-specific simulations of blood flow.
RESULTS: Four examples of grid reconstruction and blood flow simulation for patients with ruptured aneurysms were validated with angiographic and operative findings. The ruptured areas were correlated with areas of high fluid-induced wall-shear stress.
CONCLUSION: This approach promises to be a practical tool for planning treatment and follow-up of patients after neurosurgical or endovascular interventions with 3D angiography. The proposed commercial packages or conceptually similar ones seem to be relatively simple and suitable for direct use by neurosurgeons or neuroradiologists.
The treatment of vascular diseases of the brain requires an understanding of hemodynamic factors that play an important role in their development. Numerous studies have been conducted to understand the initiation, progression, and rupture of intracranial aneurysms because of their fatal outcomes (1). Researchers have used tubes made of rigid glass (2, 3), acrylic (4), or silicon rubber (5, 6) for in vivo works in animal aneurysmal models (7) and human anatomic replicas of cerebral vessels imitating real aneurysmal geometries (5, 6). Simple aneurysmal geometries have been studied by using computational fluid dynamics (CFD) to understand the properties of blood flow around aneurysms (8–15).
Tremendous developments in computer hardware and software during the last decade have made it more feasible to create a user-oriented computational system to reveal the individual patterns of hemodynamic flow in patients with cerebrovascular diseases. These systems aim to display individual physiologic variations in a practical and time-efficient way and provide a bridge between medical professionals and flow dynamicists. The present study may be considered as a step toward this goal. It focused on detailed anatomic reconstructions of cerebral vessels with complex geometry to serve as accurate 3D grid models (computational replicas) for computer simulations of their blood flow.
The key element of such an image processing and computational system is the extraction of the vascular luminal surface from medical image data; the term segmentation is traditionally used for this procedure. The subsequent steps—volume mesh generation and flow modeling—are traditional and well-established procedures in CFD. A few approaches to segmentation are known from the literature. The initial stage in most of them is the performance of separate luminal segmentation for each 2D image or data section. At the next stage, once the series of lumen contours is obtained, the luminal surface is reconstructed by using splines (16), contour tiling (17) or other similar methods. The main disadvantage of this rather sophisticated approach is that it involves a great deal of manual, time-consuming work, especially in complex geometries with branching vessels (16). No integrated, commercially available software packages seem to offer such segmentation methods. In most cases, researchers use codes developed in-house or combinations of commercial codes, libraries, and in-house developments (8, 18, 19). Computer-aided drafting (CAD) systems, which are fairly difficult to learn and operate, are often involved (18, 19). Thus, it is not easy for clinicians to implement such methods and use them in their daily practice if they do not have substantial knowledge of computer graphics, computational mathematics, and related fields.
It is generally obvious that a direct 3D segmentation technique (without resorting to 2D contours) allows a higher degree of automation (20, 21). An interesting and time-efficient virtual balloon method (22) has been proposed; in it, a spherical balloon with a triangulated surface is inserted inside the lumen and then inflated to assume the shape of the lumen. At present, implementation of the technique requires its programming from scratch. It also remains to be seen how it would perform for really complex geometries; the example of a branching vessel given in reference 22 is fairly simple.
We sought to determine how 3D imaging data collected in DICOM format can be used to create numerical grids for computer simulations of blood flow in a relatively simple way that non-CFD specialists could perform after minimum training. To achieve this goal, we used well-established, commercially available software packages, particularly Advanced Visual Systems/Express software, to extract luminal vessel surfaces; this was done with the easy and automatic procedure of isosurfacing at an operator-specified gray-scale value. This approach also belongs to the direct 3D segmentation methods, which immediately result in a triangulated 3D luminal vascular surface.
Methods
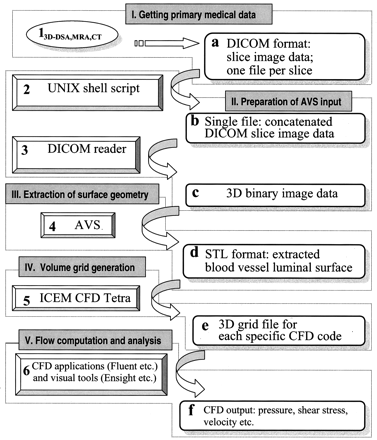
The flowchart of patient-specific computational grid reconstruction and blood flow numerical simulation in Figure 1 indicates the main tools (numbered 1–6) of the procedure and the respective output formats (a–f). The whole process consists of five logical steps (I–V). In step I, primary medical images in DICOM format are obtained. In step II, they are transformed into a format suitable for the software that will be extracting the luminal surface of the blood vessels of interest in step III. In step IV, the surface data are then imported by a grid generator, which creates a volume grid. The resulting grid model is used at step V for the numerical simulation of blood flow.
Flowchart of patient-specific segmentation, volume grid generation and blood flow analysis shows software tools (1–6) and output formats (a–f). I–V denote major stages of the procedure.
Rotational Digital Subtraction Angiography:
We obtained 3D datasets (Advantx UNV; GE Medical Systems, Milwaukee, WI) from rotational series consisting of two rotations. The first rotation provided the subtraction mask. The C-arm was rotated 200° in 5 seconds at the exposure rate of 8.8 frames per second. A total of 44 images with a matrix size of 512 × 512 pixels were acquired. The second rotation was performed simultaneously with the administration of contrast material. All 88 images were immediately transferred via our network to a workstation (Advantage Unix; GE Medical Systems) for volume analysis. A 3D reconstruction algorithm based on the algebraic reconstruction technique was used to digitally produce 3D digital subtraction angiography (DSA) images (Fig 2A and B) on the workstation within 8 minutes. Algorithms were maximum intensity projection (MIP) and surface-shaded display (SSD) at an isosurface with a mean threshold value of 1100 H.
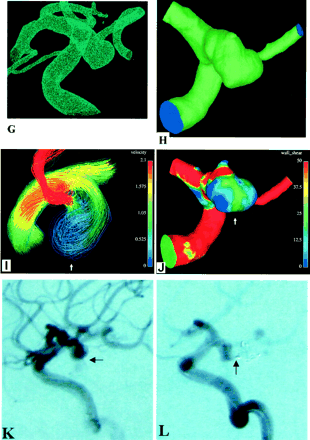
Data transformation from an angiographic image into a computational grid model.
A and B, 3D DSA images (different views) of a posterior communicating artery aneurysm.
C, Typical setup for reformatting of the angiographic image into 585 secondary DICOM sections in a 13-cm displayed field of view.
D, Sequential secondary DICOM sections. The respective files are concatenated before processing with DICOM reader (X) MedCon.
E, 3D gray-scale raster image produced by (X) MedCon and imported by AVS/Express. Columns are patient data and image parameters still present in the file.
F, Result of image manipulations with AVS/Express. ROI is cut out and the luminal vascular surface is identified with a gray-scale isosurface value of 1500. This ROI includes the aneurysm and its small branching vessel.
G, AVS/Express STL file containing the surface mesh is imported by using the ICEM CFD Mesh Editor and Tetra grid generator. These tools allow us to further remove unnecessary parts, manually repair and smooth the surface mesh, close inflow and outflow boundaries, and generate the volume grid.
H, Final computational tetrahedral grid model for blood flow simulation with Fluent or another suitable software.
I, Typical instant streamlines colored by velocity (in m/s) show that the entering bloodstream hits the aneurysm wall at the angiographically determined rupture area (arrow).
J, Typical instant wall shear-stress distribution (Pa) shows a local shear-stress maximum where the aneurysm ruptured (arrow).
K, Arterial-phase 2D DSA image shows escape of a linear stream of contrast agent into the subarachnoid space (arrow).
L, Arterial-phase 2D DSA image obtained during endovascular intervention shows escape of the coils through the aneurysm rupture (arrow).
The image displayed on the monitor was subjected to reformatting into transverse regularly spaced sections (Fig 2C). The batch function of the volume analysis allowed us to set up this set of sections rapidly. It was possible to preview the set as an animated sequence (movie loop) and save it on the image disk as sections in secondary DICOM format (Fig 2D). At the end of this stage, a separate data file for each section was generated. The file contained image data and other relevant information, such as the image size and patient’s name.
Larger numbers of sections and decreased spaces between them improved the final mesh quality. In our experience, the number of sections for 3D DSA should be in the range of 300–700 sections, with a 0.1–0.2-mm distance between the sections and a 0.3–1-mm section thickness (equal to 1 voxel). Section sets of less than 300 images were not promising in terms of final computational mesh quality.
MR Angiography
3D time-of-flight (TOF) MR angiography (MRA) was performed by using a 1.5-T MR imaging system (Signa Horizon; GE Medical Systems). A standard head coil was used for imaging of the head (Fig 3A). 3D TOF MRA was performed by using the following imaging parameters: TR/TE, 30/3.2; flip angle, 20°; section thickness, 0.8 mm; slab thickness, 64 mm; matrix, 256 × 256; and field of view, 16 cm.
Examples of four vessels reconstructed from MRA image and CTA data.
A, MRA data of four vessels with basilar top aneurysm (arrow).
B, Surface grid reconstruction of MRA image data. Note the inferior quality of this grid, as compared with that obtained from 3D DSA and multiple defects in the vessel walls.
C, Surface grid reconstruction (STL file) from CTA of four vessels of a normal circle of Willis. Note the reconstructed skull base requiring manual removal during mesh generation.
CT Angiography
CT angiography (CTA) was done by using a helical CT scanner (LightSpeed Plus-U; GE Medical Systems) with multidetector-row capability (where one scan equaled eight sections). The data presented in Figure 3 were obtained by using a section thickness of 1 mm with a 0.63-mm interval between the sections and a table speed of 8.75 mm/s (140 kV, 180 mAs). Zero-degree table and gantry tilt were used. Sections inDICOM format were acquired with a 512 × 512 matrix. Scanning was started at the C1 level and continued cranially parallel to orbitomeatal line to the skull vertex during the intravenous injection of contrast material at a rate of 3 mL/s.
The digital images and the respective files obtained so far could not be directly used for grid generation. The luminal surface of blood vessels was extracted from them in the format suitable for import by grid generators. This was done, for instance, by using the Advanced Visual Systems/Express (AVS/Express Visualization Edition, version 5.1). Step II and tools 2 and 3 of our procedure (Fig 1) were needed to convert our files into a proper format for AVS/Express input.
Merging of Section Files and DICOM Reader Software
First (Fig 1, tool 2), all DICOM files were combined into a single one, a standard operation for any computer operating system (eg, Unix, Windows, Mac OS). In the present work, this was done on a Unix computer with the concatenate command. With Microsoft Windows, the copy command allowed us to perform such file merging.
Second, (Fig 1, tool 3), the resulting single file was imported by using the X-windows medical image conversion utility (X) MedCon (version 0.5.10; Erick Nolf, Ghent University Hospital, Ghent, Belgium). The conversion utility always used original image dimensions and pixel values. This DICOM reader could output files in raw binary or ASCII formats. The binary output format included binary image data with all other information (eg, image size, patient’s name) contained in the original section image files. This additional information was to be cut later by using AVS/ Express. The resulting file at this stage contained a 3D raster gray-scale image (Fig 2E). (More details can be found at http://xmedcon.sourceforge.net.)
AVS/Express Visual Development Tool
The main role of the AVS/Express visual development tool (AVS, Waltham, MA) (Fig 1) was to define the region of interest (ROI) and to extract the luminal vascular surface from the 3D raster gray-scale image obtained at the previous stage (Fig 2). Detailed information about AVS commands may be obtained at www.avs.com.
Using the AVS isosurface command, we could extract the luminal vascular surface, triangulating it and writing into a file in stereolithography (STL) format. It used voxel intensities ranging from 0 to 4000. The procedure was fully automatic and based on picking up the data corresponding to some specified fixed value and connecting the respective points, thus forming surface triangles. In our experience, the specific gray-scale isosurface value corresponding to the luminal vessel surface could be determined by trial and error, aiming at the best appearance of the surface, in a range from 1100 to 1800 for 3D DSA data and in a range of 200–400 for MRA and CTA data. The STL format could be used as geometry input format in most modern commercial grid generators (Figs 2F, 3B, and C).
Measurements of maximum aneurysmal diameters, aneurysmal neck diameters, diameters of parent arteries, and other dimensions were performed on the luminal vascular surfaces in the 3D DSA images and their respective reconstructed meshes. The comparable measurements were statistically analyzed by using multiple regression analysis (StatView, version 5.0.1; SAS Institute, Cary, NC). The error probability values (P < .0001) and the estimated standard error (SE = 0.007) were calculated.
Grid Generator
The next stage (Fig 1, stage IV) was volume grid generation. The grid generation software (ICEM CFD version 4.1; ICEM CFD Engineering) was used to divide our model into tetrahedral cells. (Tetrahedral grids are widely used in CFD for computational models of complex shape.) The Mesh Editor and Tetra tools allowed us to cut additional unnecessary parts not related to our ROI to close the computational domain to define inlets, outlets, and wall boundaries (Fig 2G and H). Interactive modifications of the individual grid node coordinates could be done as well to eliminate unneeded small branches and false vessel connections. Finally, mesh smoothing further improved grid quality. The grid generator also allowed us to construct a triangular, prismatic, layered mesh representing vascular walls of finite thickness. This was needed for coupled flow-dynamic and elastodynamic simulations that took into account the deformations, stresses, and displacements of the vessel walls (Fig 4). (Further details can be found at www.icemcfd.com.)
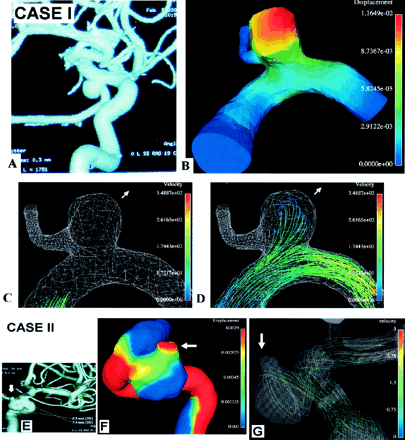
Computations for grid models with moving walls. Case I: A, 3D DSA image of a nonruptured internal carotid–posterior communicating aneurysm. B, Displacement (in mm) of the aneurysm wall at the systolic peak. Red is maximal displacement. C and D, Movie frames illustrate deformation of the aneurysm from early systole (C) to midsystolic peak (D). Arrow indicates the direction of movement (and possible future growth). Bloodstream enters the aneurysm, hits its wall, decelerates (note change in color; velocity in cm/s), and exerts pressure resulting in maximal displacement. Case II: E, 3D DSA image of a nonruptured carotid cave aneurysm. F, Displacement of the aneurysm wall at the systolic peak. Red is maximal displacement at the nonruptured aneurysmal bleb (arrow). G, Typical instant streamlines show that the entering bloodstream hits the aneurysm wall at the angiographically determined bleb (arrow), exerting pressure that results in maximal displacement.
The number of grid nodes or tetrahedrons was chosen as a reasonable compromise between better accuracy and shorter computational time of subsequent simulations. In the ICEM CFD grid generator, a nondimensional parameter Tetra determined the size of tetrahedral mesh units to be generated and, hence, the number of grid nodes, the mesh resolution, and the accuracy of the subsequent calculations. Test computations were performed for the same model with different Tetra values: 1.0, 0.5, and 0.25. It was found that the Tetra value 0.5 was small enough to get a reasonably converged solution (ie, further reduction of the parameter did not lead to considerable changes in the solution) within acceptable computational time. The numbers of nodes and tetrahedrons in the grids used to compute the cases presented in Figures 2 and 5 were within the ranges 26,000–48,000 and 170,000–285,000, respectively. The prismatic-tetrahedral grids in Figure 4 contain 7049 (case I) and 17,060 (case II) nodes.
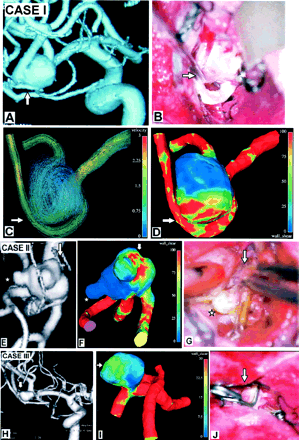
Computational results for grid models with rigid walls compared with operative photos and 3D DSA images. Case I: A, 3D DSA shows a ruptured middle cerebral artery (MCA) bifurcation aneurysm. B, Operative photo shows the aneurysm and a curved branch coming from it, the lower trunk of the MCA. Note a surgical instrument pointing to the ruptured zone on the aneurysm wall (arrow) under the genu of the lower trunk of the MCA. C, This zone faces the blood stream entering the aneurysm (arrow, velocity in m/s). D, Wall exposed to high shear stress (arrow, units of Pa). Case II: E, 3D DSA of a ruptured MCA bifurcation aneurysm with multiple blebs. F, Typical instant wall-shear-stress distribution (Pa) shows a local shear-stress maximum where the aneurysm ruptured (arrow in F). Largest bleb (star) in the low-shear-stress area of the aneurysm wall. G, At surgery, this was not ruptured and had an intact wall. Dome blebs in the high shear stress area (arrow) in front of the coming bloodstream were the ruptured ones and were tentatively clipped (arrow). Case III: H, 3D DSA image of a small, ruptured MCA bifurcation aneurysm. I, Typical instant wall-shear-stress distribution shows a local shear-stress maximum where the aneurysm ruptured (arrow). 3D orientations of the aneurysm are similar in I and J, an operative photo showing the aneurysm in the sylvian fissure after proximal clip placement of the MCA and a thin-walled, ruptured area (arrow) where the aneurysm had maximum local shear stress.
Computational grids obtained from stages I–IV (Fig 1) could be applied to numerical simulations of blood flow in the respective geometry by using CFD software (Fidap; Fluent Inc., Lebanon, N.H.).
Flow Modeling
The unsteady 3D incompressible Navier-Stokes equations are widely used for blood flow simulations. Blood is usually considered a Newtonian fluid; this is a fairly good approximation for large-bore vessels. Our simulations were performed with the following material constants: blood density, 1060 kg/m3; and blood dynamic viscosity, 0.004 Poiseuille.
To achieve truly patient-specific modeling, the boundary condition at the inflow boundary was based on the pulsatile periodic flow rate obtained during sonography of intracranial vessels. Because the governing equations and boundary conditions included only the pressure gradient, the simulation produced relative pressure values to be considered with respect to a basal pressure.
The unsteady flows in aneurysms were computed for an interval of 3 seconds (over three cardiac cycles). The results corresponding to the last, third cycle were considered independent of the initial conditions and used for flow analysis. We performed several computations for the same model with different time steps: 0.1 second (30 steps), 0.025 second (120 steps), and 0.01 second (300 steps). As long as the grid-converged solution was obtained (ie, the grid was fine enough), the time step values did not dramatically influence the results at a certain instant of the cardiac cycle (eg, at the systolic peak). The time step of 0.025 second seemed to provide a reasonable compromise in terms of accuracy and computational time and for plotting and statistical analysis.
As to the walls of the vessels, two main possibilities exist. The first and simplest approach was to consider them as rigid structures. The second was to account for their movement and deformation. In the latter, an elastic model was chosen, with its parameters to be determined.
Rigid Vessels
Under this assumption, any CFD code with incompressible fluid-modeling capabilities can be used. We applied Fluent software (version 6.0.12) (Fluent Inc., Lebanon, NH) to compute physiologic pulsating flows. In the code, the governing equations written in strong conservative form for mass and momentum were discretized with a finite-volume method. We chose the SIMPLE method to solve the discretized equations. To improve the convergence speed, relaxation factors were applied to velocity and pressure modifications. (Detailed information about the code is available at www.fluent.com.)
On the rigid vessel walls, the nonslip and nonpenetration conditions were applied (ie, all velocity components at the vessel walls were set to zero). For the outlet, the Fluent outflow boundary condition was used. The typical computational time on the grids just mentioned was approximately 8–12 hours on a single processor (Origin 2000; Silicon Graphics Inc).
Deformable Vessels
This model required a fluid-structure interaction approach accounting for both instantaneous fluid forces acting on the walls of vessels and for effects of the walls’ motion on the fluid dynamic field. The number of software packages that included fluid-structure interaction capabilities was relatively limited. Fidap (Fluent Inc., Lebanon, NH) code was used to carry out the simulations presented in Figure 4.
In this code, an Arbitrary Lagrangian Eulerian (ALE) algorithm was used. This sought, at each time increment, the convergence of three blocks of equations describing blood dynamics, stresses in vessels’ walls, and mesh movements (23). The only Fidap option for vascular walls was a linear elastic homogeneous approximation. The following elastic material constants were used: Young modulus of 2.7 Mpa and Poisson coefficient of 0.45 (18). The cases in Figure 4 took more than 4 days to compute on a single processor (Origin 2000; Silicon Graphics Inc). (A description of Fidap can be found at www.fluent.com.)
Flow Visualization
Fluent, Fidap, and other CFD software packages have their own visualization tools that are sufficient in many cases. However, specialized postprocessing software might offer additional useful options. For instance, we used EnSight (version 7.3.0; Computational Engineering International Inc., Apex, NC), which was general-purpose postprocessing software used in engineering and research and available for all major computer platforms. This was used to create computer animations (movies) of unsteady blood flow through aneurysms based on Fluent and Fidap results (Fig 5). (Details can be found at www.ensight.com.)
Results
Figure 2 shows data from a patient with ruptured internal carotid–posterior communicating artery aneurysm and illustrates the whole procedure of computational analysis from 3D DSA to CFD results. The ruptured area was depicted by using angiography (Fig 2K and L). Comparison with the simulation results allowed us to conclude that it corresponded to the area facing the bloodstream entering the aneurysm. The aneurysm wall served as an obstacle decelerating the entering stream (diminishing its velocity) and deflecting it along the wall. This was accompanied by a persisting local fluid-induced wall shear-stress maximum in the area hit by the stream; this might have been one of the reasons for aneurysm rupture.
Figure 3 illustrates surface grid extractions from MRA of the circle of Willis and CTA. One image shows multiple defects in the wall of the basilar artery aneurysm that made surface mesh repair and volume grid generation more time- and labor-consuming than they would have been with “clean” 3D DSA images. Nevertheless, there were no fundamental difficulties, and surface grid reconstruction for sparsely sampled MRA-based objects was attainable with the proposed approach. CTA showed promising mesh quality that may be useful for studying flow dynamics of the intracranial vessels. However, manual removal of the reconstructed skull base bone was necessary.
Figure 5 illustrates another attempt at computational diagnosis of the rupture area of MCA aneurysms, with subsequent surgical validation. Similar to a previous case (Fig 2), the ruptured area corresponded to the area where the entering blood stream first hit the wall (at an angle). Again, high wall-shear stress was seen in this area; this might have been the reason for rupture at this location.
Case I in Figure 4 (nonruptured internal carotid–posterior communicating artery aneurysm) represented successful 3D modeling that accounted for vascular movement and deformation by using Fidap. In correspondence with the findings illustrated in Figures 2 and 5, this figure identified the maximum area of displacement as the area hit by the blood jet entering the aneurysm. The aneurysm was likely to grow in this direction. It was also a primary suspect for the location of possible rupture or bleb formation, as shown in case II in the same figure (nonruptured carotid cave aneurysm). These findings confirmed that the maximum area of wall displacement is located at the angiographically determined bleb in the aneurysmal inflow zone.
Discussion
The method for anatomic reconstruction of cerebral vessels in the form of computational replicas should work for a broad spectrum of medical imaging techniques, the availability of which varies from one medical center to another. Replicas were obtained from all currently available modalities of cerebral angiography, such as noninvasive screening MRA and CTA, which can sometimes replace 3D DSA in diagnosing intracranial aneurysms (24, 25) and also the invasive, highest-quality 3D DSA. Therefore, our approach was general: It worked with any 3D image data in DICOM format as the source of original information, and it could produce grid output for virtually any commercial CFD software.
Segmentation (Surface-Extraction) Techniques
In our approach, the entire set of cross-sectional images (sections) obtained from angiographic machines was immediately fused into a single 3D DICOM image by means of simple file merging. The DICOM reader then converted the DICOM file into a binary format suitable for use with image processing and visualization software, such as AVS/Express. Therefore, in AVS/Express we directly manipulated the original source output of the angiography machines without any modifications and used it to extract the luminal surface. This approach substantially contributed to the simplicity and stability of operations and minimized possible errors of image interpolation.
Direct 3D segmentation in AVS/Express by means of isosurfacing is simple and fully automatic and requires minimal effort; this is in contrast to the sophisticated image-segmentation methods based on 2D (section-by-section) segmentation with the subsequent reconstruction of 3D luminal surface geometry (26–30). These methods usually require a computer graphics or computational mathematics specialist to accomplish them. Isosurfacing is conceptually close to the virtual balloon inflation technique (22), which is also based on direct 3D segmentation.
The average time of image segmentation from DSAs or MRAs into luminal surface meshes (STL files) is about 30 minutes. The resulting surface meshes from densely sampled high-spatial-resolution data (eg, DSA images) are of high quality. They need no or only minor manipulations in the mesh generator before volume mesh generation (which is an automatic procedure). Sparsely sampled objects (eg, MRA images) have lower spatial resolution and therefore result in a lower-quality surface mesh. These need more effort from the examiner to remove image artifacts and to repair and smooth the surface mesh before tetrahedral mesh generation (26). Future advances in angiographic technology to further improve DSA image quality will certainly simplify and improve the accuracy of luminal surface segmentation by means of isosurfacing.
3D images are manually optimized to define the vascular luminal surface before volume grid generation. Therefore, correction for the penumbra effect (unsharpness of edge determination due to diminished contrast resolution as the luminal vascular boundary is approached) is operator-dependent with this method.
Our experience with segmentation by means of isosurfacing in AVS shows that obviously false communications (eg, between small arteries and an aneurysm) may arise when we use an isosurface value that otherwise seems optimal for the most accurate representation of the luminal surface. Although such false connections can be eliminated by increasing the isosurface value, we recommend keeping this value and removing it later in the ICEM CFD grid generator and mesh editor.
The choice of ROI primarily depends on the examining physician and on what he or she wants to achieve from the whole procedure. At best, we know only the mean flow parameters in vessels as a function of time. This is why we should set our inflow and outflow boundaries “far enough” so that our insufficient knowledge does not influence the flow in the aneurysm under study. The uncertainties in the inflow-outflow parameters are at least of the same significance as that of errors produced by the location of inflow-outflow boundaries. However, physicians using CFD should have some knowledge of incompressible fluid dynamics, or they should solicit help from a fluid dynamics specialist to learn about the possible strong fluid dynamic effects proximal and distal to the aneurysm; such effects are due to factors such as severe arterial curvature, which may cause large secondary flows. The inflow boundary should be set within unidirectional fluid flow without any vortices or secondary flows.
Special attention should be paid to cutting out ROI and downsizing the image. Minimization of the ROI is important to decrease computational time (for both grid generation and computation itself), making it possible to finish the patient-specific image processing and computational procedure in 1 day. In our experience, the average time needed for calculation of the ROI limited to the aneurysm zone (about 5 hours) was shorter than that needed to calculate the whole parent artery with the aneurysm (about 2 days), when the results inside and near the aneurysm are confirmed to be the same for both ROIs. Nevertheless, these considerations about the possible influence of inflow-outflow boundaries on the results should be always kept in mind.
CFD by Physicians
The knowledge and skills needed to conduct CFD studies—including some elementary background in incompressible fluid mechanics and computational methods—are comparable to those needed to conduct, understand, and interpret radiologic studies (eg, MR, CT, SPECT, and PET images). Therefore, physicians themselves will undoubtedly perform CFD analysis in the future. In the mean time, because such CFD studies are still a relative novelty under development, they should be initially conducted under the supervision of a fluid dynamicist to establish a reliable technique and to correlate the results with radiologic or operative information. Now we rely on a set of commercially available software packages that might soon be replaced by a single, integrated technician-operable software package. Physicians should not straightforwardly rely on the first results that they receive from CFD computations to detect the possible location of an aneurysm rupture. A comparative, blinded study should be first conducted in any institution looking for applications of CFD before the whole numerical procedure is proved correct and time-efficient. Only after that can this code be used more widely in clinical work.
CFD as a Useful Clinical Tool
Applications of CFD as an assisting tool for studying patient-specific hemodynamics are becoming more practical. Several clinical applications of CFD in cerebral aneurysms of real patients have been described (31, 32, 33). Detection of the rupture area of intracranial aneurysms before surgery is important for every neurosurgeon. Although somewhat simplistic modeling that assumes rigid vessel walls may be promising for this purpose in some cases (such as those shown in Figure 5) because of the relatively short computational time. In these cases, the whole computational analysis lasted an average of approximately 8 hours, which makes it possible to treat patients the same day as an acute hemorrhage; this method provides CFD results, if needed, before surgery.
For the cases presented in Figures 2 and 5, the ruptured area of the aneurysms geographically corresponded to the area in which the bloodstream entering the aneurysm hit its wall. This area also corresponded to relatively high pressure- and fluid-induced wall shear stress in the aneurysms. This finding would not have been possible without angiographic or operative confirmation. In general, when a blood jet impinges on an aneurysm wall, there is a stagnation point at which pressure is maximal but wall shear stress is zero. Around this localized high-pressure spot is a large area of high wall shear stress caused by the bloodstream turning along the aneurysmal wall; this is where rupture happens, as seen in our cases.
In realistic acrylic aneurysmal models, Tateshima et al (4) found that the bleb of an aneurysm is exposed to a shear stress higher than that of any other measured point. Wall shear stress is a dynamic frictional force induced by a viscous fluid moving along a surface of solid material. The endothelium regulates local vascular tone by releasing vasodilator and vasoconstrictor substances (29, 34). It is sensitive to changes in oscillating wall shear stress, which has stronger biologic influence on vessels by impinging on various endothelial functions than direct mechanical force (29, 34). Increased wall shear stress is regarded as a major factor in the development and growth of cerebral aneurysms (27, 30). Increased wall shear stress caused by increased flow velocity stimulates the release of endothelium-derived nitrous oxide, which is known as a strong vasodilator and also is a potential factor in arterial wall degeneration (27, 28, 34, 35). Therefore, a local increase in wall shear stress may cause local dilatation and degeneration of arterial walls.
Limitations of CFD
Any simulation study is based on a number of simplifying assumptions, such as considering blood as a Newtonian fluid, ignoring the real thickness of the aneurysmal wall, neglecting effect of gravity and position, and others. The validity of these assumptions seem to be of secondary importance compared with the influence of the geometry and the pulsating nature of blood flow; these are the most important factors for predicting possible aneurysmal growth and rupture.
In addition to the model assumptions, another limitation of computational analysis is that it is not possible, with current computer resources and time limitations in clinical practice, to evaluate the influence on the aneurysm hemodynamics of all model parameters (eg, heart rate and rhythm, blood pressure) and their variations in time. Although computer modeling allows for easy manipulation of these parameters, at present we usually deal with a few representative cases revealing only the most essential hemodynamic features of the aneurysm under study. Full parametric studies are rarely done. It is also wise to be aware of the actual accuracy of different stages of computer simulation and to keep it consistent. For instance, it may not make sense to compute flow fields accurate to 1% if the input geometry is accurate to only 10%.
Model validation is an essential, ever-present component of CFD simulation work. Any opportunity to compare fluid dynamic data from laboratory and clinical studies with simulations should not be neglected. This is especially important for patient-specific analysis in which faithful representation of the geometry is required to achieve meaningful results. As stated in reference 36, “improvements in laboratory and clinical fluid dynamic measurement capabilities can have a direct, positive impact on the accuracy and usefulness of CFD simulations by helping to identify the relevant sources of error so improvements could be made.”
Models of Rigid and Deformable Vessels
Simulations with deformable vessels are more realistic, from a general point of view. However, their major disadvantage is a long computational time (more than an average of 7 days for the cases presented in Figure 4). Another restriction is the limited number of elastic models available in commercial CFD codes. For instance, linear homogeneous elastic behavior of the wall is the only option currently available in Fidap. Nevertheless, studies such as those in Figure 4 may provide a basic understanding of the hemodynamic behavior of geometrically similar intracranial aneurysms. It is reasonable to expect the eventual elimination of these deficiencies with further progress in both computer hardware and software.
Conclusion
This study was concerned with developing an efficient technique for the automatic creation of vascular computer replicas from medical imaging sources. We sought a practical method that neurosurgeons or neuroendovascular surgeons could use. Such a technique should simplify the geometry under consideration to decrease the computational time needed for CFD analysis and still preserve the essential features. Although we were mainly interested in cerebral aneurysms, this approach can also be used for other conditions, such as arteriovenous malformations (AVMs), AVM flow-induced aneurysms, and atherosclerosis in intracranial and extracranial vessels, among others. Patient-specific computer modeling, combined with information from other imaging modalities, may provide important insight into flow dynamics before and after surgical or endovascular treatment.
Acknowledgments
We express our deep thanks to Mr Hiroyuki Shimura, Graphics System Analyst, SGI Japan, and Ms Midori Ooki, Research Center of Computational Mechanics Inc, Tokyo, Japan for their help in fulfilling this work.
Footnotes
Supported by the Government of Japan as a part of the 21-Century Center of Excellence (COE) program.
Presented in part at the 19th Annual Meeting of the Japanese Society of Intravascular Neurosurgery, Yokohama, Japan, November 17, 2003.
References
- Received October 6, 2003.
- Accepted after revision January 15, 2004.
- Copyright © American Society of Neuroradiology