Abstract
BACKGROUND AND PURPOSE: Chronic hydrocephalus is associated with dilated ventricles despite a normal intracranial pressure. In idiopathic intracranial hypertension, the ventricles are normal despite an elevated intracranial pressure. This apparent paradox has largely remained unexplained. It is suggested that a pressure difference between the superficial and deep venous territories of the brain could account for the variation between the 2 diseases. The purpose of this paper is to investigate the cause of this pressure difference.
MATERIALS AND METHODS: Using MR phase-contrast imaging, we calculated the hydraulic diameters of the sagittal and straight sinuses in 21 patients with hydrocephalus, 20 patients with idiopathic intracranial hypertension, and 20 age-matched controls. The outflow resistance of each sinus was estimated using the Poiseuille equation. The outflow pressure was estimated using the flow data. A smaller subset of the patients with hydrocephalus had these studies repeated after successful shunt insertion.
RESULTS: In hydrocephalus, the sagittal sinuses were 21% smaller than those in controls (P < .001); the straight sinuses were not significantly different. In idiopathic intracranial hypertension, both sinuses were not significantly different from those of controls. The pressure drop from the sagittal sinus to the end of the straight sinus was elevated by 1.2 mm Hg in hydrocephalus (P = .001) but not significantly different from that in controls in idiopathic intracranial hypertension. Shunt insertion dilated the sagittal sinuses in hydrocephalus, leaving them 18% larger than normal and eliminating the transvenous pressure change.
CONCLUSIONS: There is a transvenous pressure difference in hydrocephalus that is absent in idiopathic intracranial hypertension. This difference is eliminated by shunt insertion. The findings may have a bearing on ventricular dilation.
ABBREVIATION:
- IIH
- idiopathic intracranial hypertension
It has been estimated that >30,000 shunt procedures are performed in the United States every year to treat hydrocephalus.1 This is despite a lack of understanding of what causes the disease or how a shunt exactly treats the condition. In chronic hydrocephalus, there is deformation of the brain parenchyma, which requires an expenditure of energy. In a hydraulic system, energy expenditure requires a pressure difference. It is assumed that a shunt treats this pressure difference. However, previous searches for a pressure drop between the ventricles and the subarachnoid space2 and the brain parenchyma3 or a pulse pressure difference4 have been unsuccessful. Nevertheless, previous work by one of the current authors suggests that a pressure difference may exist between the superficial and deep venous territories in normal pressure hydrocephalus,5 and this could supply the energy required for ventricular dilation. In idiopathic intracranial hypertension (IIH), the ventricles do not dilate; therefore, a pressure difference should not exist in this disease.
Recently, a 25% reduction in the sagittal sinus cross-sectional area in hydrocephalus but no change in the IIH sagittal sinus cross-sectional area has been found.6 This finding would imply that an increase in pressure difference between the torcular and midsagittal sinus could exist in hydrocephalus but not in IIH. The purpose of the current study was to measure the sagittal and straight sinus cross-sectional areas and circumferences to calculate the hydraulic diameter and resistance of each. These data, together with blood flow data, will allow an estimate of the pressure difference from the midsagittal sinus to the end of the straight sinus (ie, the transvenous pressure difference). Review of a subset of the patients with hydrocephalus post-shunt insertion may shed light on the therapeutic effect of this procedure.
Materials and Methods
Subjects
In a previous study undertaken by one of the authors,7 there were 21 patients with chronic idiopathic hydrocephalus (mean age, 45 ± 10 years; 7 women and 14 men). There were 20 controls (mean age, 44 ± 10 years, with 8 women and 12 men).7 These patients were entered into the current study, and the clinical data for these patients can be reviewed in the prior publication.7 In 8 of these patients, the study protocol was repeated following shunt insertion. The average valve pressure set by the neurosurgeon was 105 ± 23 mm H2O. The age of these patients was 30 ± 10 years, with 3 males and 5 females. The follow-up was 1.7 ± 2.7 years later. Twenty patients with idiopathic intracranial hypertension were entered from a prior publication undertaken by one of the current authors.8 There were 18 women and 2 men of average age 40 ± 11 years.8 In all 20, there was an increase in CSF opening pressure above 25 cm H2O, with the mean pressure being 31 ± 4 cm H2O. There was a normal ventricular size and no apparent cause for the pressure rise in these patients. Informed consent was obtained for all patients entering the original study,7 which was given the authorization HNEHREC 07/03/21/5.03. Informed consent was also obtained for all patients entering this study. The study was reviewed by the Hunter New England Human Research Ethics Committee with authorization HNEHREC 16/06/15/5.06.
MR Imaging Technique
All patients were scanned on a 1.5T superconducting magnet (Verio; Siemens, Erlangen, Germany). In all patients, a standard brain MR imaging consisting of T1 sagittal, T2 axial, FLAIR axial, and diffusion-weighted axial images was performed. A time-of-flight MR venogram was obtained in the off sagittal plane with a slice thickness of 3 mm. An MR phase-contrast flow-quantification sequence was acquired with retrospective cardiac gating. The TR was 26.5 ms; TE, 6.9 ms; flip angle, 15°; slice thickness, 5 mm; matrix, 192 × 512; FOV, 150 mm; with a single excitation. The velocity-encoding value was 40 cm/s. The plane was selected to pass through the sagittal sinus 3 cm above the torcular and through the midpart of the straight sinus. The MR imaging was sourced from the hospital PACS; therefore, all measurements were performed on the original data. In all patients and controls, the cross-sectional area and wetted circumference of the sinuses were measured manually from the magnitude images of the flow-quantification series by one of the authors (G.A.B.) using the workstation measurement tool. The straight sinus length was measured manually from the MRV images from the junction with the vein of Galen to the torcular using the workstation curved length tool. The sagittal sinus length was measured from a point in the sagittal sinus that was in the same horizontal plane (the patient being supine) as the end of the straight sinus.
Analysis
The hydraulic diameter of each venous sinus segment was calculated using the formula:
where Hd is the hydraulic diameter, A is the cross-sectional area of the sinus, and Circ is the wetted circumference of the sinus.9 The resistance of each sinus was calculated using the Poiseuille equation:
where R is the resistance of each sinus, μ is the viscosity of blood (assumed to be 0.0035 Pa × s10), L is the measured length of each sinus, and r is the sinus radius, which is taken to be the hydraulic diameter divided by 2. The pressure drop through the sagittal and straight sinuses (ΔP) for each subject was calculated by multiplying the resistance value by the sinus flow (Q) in each instance:
This was converted from pascals to millimeters of mercury for ease of discussion.
Statistical Analysis
Normality for all data was tested using a Shapiro-Wilk test with significance set at .05. Group means and SDs were obtained for each of the measurements. A nonpaired t test, with a P value < .05, was used to indicate statistical significance. A paired t test was used for the patients with hydrocephalus pre- and post-shunt insertion. All statistical analysis was performed using Matlab software (MathWorks, Natick, Massachusetts).
Results
Measurements
The sinus hydraulic diameter, resistance, and pressure results are summarized in On-line Table 1. The pre- and postshunt results are summarized in On-line Table 2.
The mean sagittal sinus lengths for the controls and patients with hydrocephalus and IIH were 13.1 ± 1.2 cm, 13.5 ± 2.1 cm, and 13.1 ± 1.5 cm, respectively, and were not significantly different. In hydrocephalus, the hydraulic diameter of the sagittal sinus was reduced by 21% (P < .001) and the resistance was increased by 166% (P = .002) compared with controls. None of the other hydraulic diameters or resistances were significantly different. In controls, the sagittal and straight sinus blood flow averaged 5.7 ± 1.5 mL/s and 1.6 ± 0.5 mL/s, respectively; 4.6 ± 1.1 mL/s and 1.4 ± 0.4 mL/s in hydrocephalus, respectively; and 5.9 ± 1.3 mL/s and 1.8 ± 0.5 mL/s in IIH, respectively. In hydrocephalus, there was a 100% increase in the pressure drop across the sagittal sinus and a 38% decrease in the pressure in the straight sinus (P = .01 and .04). This result led to an increase in a sagittal sinus-to-straight sinus pressure difference of 1.2 mm Hg (P = .001) compared with controls. In IIH, the pressure differences were not significantly different from those of controls.
Following shunt insertion, in the smaller cohort of patients with hydrocephalus, the sagittal sinuses increased in size by 49% (P = .007). This change reduced the sagittal sinus resistance by 85% (P = .05) and eliminated the transvenous pressure difference.
Discussion
The current study builds on previous work.7,8 The sagittal sinus and straight sinus blood flow data have been previously published for the patients with hydrocephalus and controls.7 The sagittal sinus blood flow has been previously published for patients with IIH.8 All other data are new to this article.
The pressure drop through a vessel can be calculated using the Poiseuille equation.11 Fall et al12 used this equation, finding the normal resistance of the sagittal sinus to be 20.1 Pa/mL/s and the straight sinus to be 40.2 Pa/mL/s. Our method varies in 2 important ways from this article. First, we measured a shorter length of the sagittal sinus because we measured the same vertical distance from the MR imaging table as the end of the straight sinus to negate the necessity of allowing for the hydrostatic pressure difference; and second, we used the hydraulic diameter rather than assuming the sinuses to be circular in cross-section (personal correspondence with Dr Baledent PhD email March 2017). The flow through a triangular tube, such as a venous sinus, is much less efficient than in a cylindric tube.13 The hydraulic diameter takes this reduced efficiency into account.9 This combination of factors gave our controls a lower sagittal sinus resistance than that of Fall et al12 of 15.9 Pa/mL/s and a higher straight sinus resistance of 108 Pa/mL/s. The sagittal sinus area and circumference have been measured by others using intravascular sonography in IIH, and the mean hydraulic diameter of 6.5 mm14 is identical to that in our control cohort, suggesting an acceptable precision in our method.
Transvenous Pressure Difference
In controls, the pressure drop across the sagittal sinus averaged 0.7 mm Hg, and the straight sinus, 1.3 mm Hg, giving a transvenous pressure difference of −0.6 mm Hg (the negative value indicating that the deep territory sinus is of higher pressure). In hydrocephalus, the average sagittal sinus pressure drop was doubled at 1.4 mm Hg. The straight sinus resistance was not significantly different from that in the controls, but the blood flow was less, giving a lower pressure drop of 0.8 mm Hg. The average transvenous pressure difference in hydrocephalus was thus +0.6 mm Hg or 1.2 mm Hg higher than that in controls. In IIH, the sinus pressure difference was not significantly different from that in controls. Therefore, an increased transvenous pressure difference correlated with dilated ventricles and a normal difference with small ventricles.
Paradox of the Change in Sinus Size in Hydrocephalus
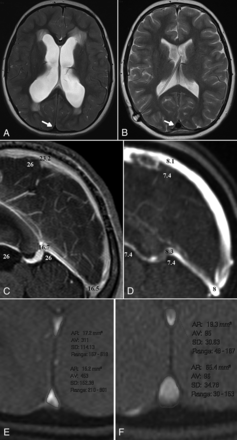
In a smaller cohort of 8 patients, the MR imaging protocol was repeated after shunt insertion. Pre-shunt insertion, all 21 patients showed small convex sagittal sinuses, similar to that in the Figure, A. Post-shunt insertion, all patients showed the free walls of the sinuses to be bowing outward (Figure, B). The change in appearance was noted to be a helpful sign that the shunt was working. The dilated sinuses looked like a filled spinnaker on a yacht (ie, the billowing sail sign; see the On-line Figure for further examples). The change in size highlights a paradox. The free walls of the sinuses sit between the CSF and the venous blood. The walls are concave when the pressure is higher in the CSF than in the lumen (positive transmural pressure difference) and convex when the pressure difference reverses.6 Thus, in the 8 patients, the transmural pressure difference reversed after the shunt insertion. The degree that the sinus wall deflects depends on the magnitude of the transmural pressure difference and the stiffness of the sinus wall (ie, the elastic modulus).6
A, A T2 image of a 16-year-old girl with idiopathic hydrocephalus. Note the transependymal CSF spread. The arrow shows the small concave sagittal sinus. B, A T2 image following shunt insertion. The valve setting was 100 mm H20. The sinus has increased in size and has convex margins (ie, the billowing sail sign). C, A postcontrast T1 reconstruction pre-shunt insertion. The white numbers are the CSF pressure from a lumbar puncture. The black numbers represent the calculated sinus pressures. The 2.8-mm Hg pressure drop from the CSF to the sagittal sinus is from a previous work.7 Note the 9.3-mm Hg pressure drop from the CSF to the vein of Galen with no sign of venous collapse. The thalamostriate vein was not compressed but had moved out of plane. D, A reconstruction from the MRV post-shunt insertion, with CSF and venous pressures appended. The CSF pressure of 7.4 mm Hg is the shunt tube setting. The sagittal sinus pressure of 8.1 mm Hg is an estimate, given the convex sinus. E, A flow-quantification magnitude image pre-shunt insertion. The straight sinus area is 17.2 mm2, and the sagittal sinus area is 15.2 mm2. F, A flow-quantification magnitude image post-shunt insertion shows the straight sinus unchanged at 19.3 mm2, but the sagittal sinus is much larger at 65.4 mm2.
In healthy controls, the transmural pressure difference is known to be 4 mm Hg, and the sinus wall bulges slightly inward, giving a cross-sectional area of 42.1 mm2.6 The transmural pressure difference in patients with hydrocephalus was previously estimated to be 2.8 mm Hg,7 with this smaller difference producing a much larger wall deflection than in the controls (see Figure, C for an example of the pressure differences).6 The inference would be that the elastic modulus of the sagittal sinus in hydrocephalus is much lower (ie, the walls are floppy), but this cannot be true. The speed of pulse wave propagation along the sagittal sinus is increased by 2.4 times in normal pressure hydrocephalus.15 The speed of a pulse wave is given by the equation V = √Eh / ρr, where E is the elastic modulus, h is the vessel wall thickness, ρ the fluid density, and r is the vessel internal radius.16 Given that the wall thickness and fluid density are constants, the ratio of the elastic modulus to the internal radius of the sinus in hydrocephalus must increase 5.8 times. The radius is reduced by 20% compared with that in controls. Therefore, the elastic modulus must be 4.6 times stiffer in hydrocephalus to account for the pulse wave velocity. The only way the sinus wall can be stiffer and yet still deflect further with a smaller pressure difference would be if the walls were irreversibly stretched. Note, post-shunt insertion, the sinuses greatly dilate with the CSF pressure set by the shunt valves in this cohort averaging 7.7 mm Hg. A normal sagittal sinus pressure is 7.5 mm Hg.17 Thus, the sinus pressure post-shunt insertion must be minimally above the CSF pressure, but the sinuses still overdilate (Figure, D–F).
Venous Territories and Pressure Differences
The venous territories drained by the sagittal and straight sinuses are known to be separate. Intracerebral venous anastomoses through the centrum semiovale toward the convexity are nonexistent or negligible in humans.18 Instead, a venous watershed exists, separating paraventricular white matter from a layer of subcortical white matter.18 Thus, a pressure difference could be maintained between the superficial and deep venous territories. The capillary and venular pressure in the brain is thought to be maintained by a Starling resistor due to the compression of the connecting veins as they pass through the subarachnoid space.19 Thus, a pressure difference in the sinuses would be irrelevant to the brain parenchyma if both brain territories had their pressures set by the intracranial pressure. However, Portnoy et al2 maintained that the Starling mechanism is absent in the deep system and the pressure in the deep parenchyma is similar to that in the dural sinuses. The current study confirms these findings. The pressure difference between the CSF and the straight sinus is high in hydrocephalus, so vein of Galen compression should be obvious. No venous compression was evident in any of the MRVs. The patient in the Figure, C had the largest CSF-to-vein of Galen pressure difference of the cohort, but no compression was seen. Thus, it appears that the reduced venous pressure in the deep sinuses is free to propagate throughout the entire deep system.
The modeling of hydrocephalus in dogs shows an increase in sagittal sinus pressure, reduced sinus compliance, and abnormal collateral veins.20 The entire sinus length was constricted in the hydrocephalic dogs,20 identical to findings in the current study.
MR elastography measures the stiffness of the parenchyma of an organ. The stiffness of the brain increases with venous compression in the neck.21 MR elastography in normal pressure hydrocephalus shows increased stiffness in the parietal and occipital lobes (drained by the sagittal sinus22) and decreased stiffness in the periventricular white matter23 (drained by the deep system22). Thus, the MR elastography suggests an increased pressure in the superficial venous system and decreased pressure in the deep system.
Is a 1.2-mm Hg Pressure Difference Enough?
The current study has a mixture of patients with active and balanced hydrocephalus, so the calculated pressure difference may be lower than if only active cases were used. Therefore, the patients with shunts with active hydrocephalus have higher transvenous pressures than the remainder of the cohort (1.5 versus 0.6 mm Hg).
Hydrocephalus is associated with CSF ventricular reflux24 and evidence of reversed aqueduct flow.25 Transependymal CSF absorption may exist in hydrocephalus, but is a 1.2-mm Hg pressure difference enough to dilate the ventricles? It has been suggested that a transmural pressure difference need not be large to dilate the ventricles.25 Kim et al26 found that the ventricular enlargement could be explained by a transmantle pressure gradient of 1.0 mm Hg, similar to the current estimate.
Studies using sagittal sinus ligation in animal models uniformly produce an elevation in CSF pressure but no evidence of hydrocephalus in the acute setting.27 Similarly, acute thrombosis of the sagittal sinus does not produce hydrocephalus despite an obvious pressure difference between the venous territories. Therefore, there must be another variable involved over and above the pressure drop.
CSF Capillary Absorption
The absorption of CSF into the capillaries requires passage across the blood-brain barrier. Hladky and Barrand28 argued that net absorption of CSF across an intact blood-brain barrier is not sustainable regardless of the hydrostatic pressure because the salt would be left behind and a rapid increase in osmotic pressure would negate the hydrostatic pressure difference within minutes. This argument suggests why ligating the sagittal sinus does not produce ventricular dilation (ie, the blood-brain barrier stays closed). In human hydrocephalus, the capillary wall shows blood-brain barrier dysfunction with increased vesicular and vacuolar transport, open interendothelial junctions, thin and fragmented basement membranes, and discontinuous perivascular astrocytic end-feet.29
Difference between Hydrocephalus and IIH
The absorption of CSF is traditionally seen to occur through the arachnoid granulations, requiring a pressure difference of 4 mm Hg.8 This pressure drop is maintained by the structural integrity of the walls of the sinuses.
In IIH, there is collapse of the sinuses below the torcular, and there is an elevation in central venous pressure due to obesity.30 The venous collapse has the effect of raising the venous sinus pressure and initially reducing the pressure drop across the arachnoid granulations so CSF absorption stops. The CSF pressure will rise until a new equilibrium is reached, where the pressure drop across the arachnoid granulations reverts back to 4 mm Hg and CSF absorption resumes at a higher overall pressure. There is no ventricular enlargement because the pressure in the deep brain parenchyma is unchanged compared with the superficial parenchyma (ie, there is no transependymal CSF absorption, and this prevents the dilation from occurring).
In hydrocephalus, there is collapse of the sagittal sinus. This sets up a pressure differential between the superficial and deep brain parenchyma. The increase in sagittal sinus pressure stops CSF absorption across the arachnoid granulations, and the CSF pressure initially rises. If the blood-brain barrier becomes deficient in the region of the subependymal white matter, then CSF can be absorbed through this route. If the CSF transependymal absorption matches CSF production, then the CSF pressure will fall back into the normal range. A small pressure difference across the ependyma will dilate the ventricles across time. The pressure in the sagittal sinus remains slightly elevated; thus, the pressure across the arachnoid granulations is reduced, and the pressure drop remains unfavorable for CSF absorption via this route. Shunt insertion eliminates the transvenous pressure difference, and the ventricles can be reduced in size because the pressure difference between the deep capillaries and CSF reverses.
Limitations
The measurements occurred in quiet respiration in supine patients. It is difficult to predict how the pressure changes would be altered in the upright position. The pressure drop between the CSF and sagittal sinus in the Figure was estimated from a previous article. The Davson equation would predict a higher pressure difference of 5–6 mm Hg.7 This would actually increase the pressure difference from the CSF to the subependymal capillaries, making ventricular dilation more likely.
Conclusions
The size of the sagittal sinus cross-section is smaller in hydrocephalus than in controls and IIH. The cross-sectional area of the straight sinus is not significantly different across groups. If one considered the sinus blood flow, the current modeling suggests a small increase in transvenous pressure in hydrocephalus but no change in IIH. This finding may have a bearing on the cause of ventricular dilation. Shunting reverses the change.
Acknowledgments
We thank Dr O. Baledent for clarifying the technique used in the article by Fall et al.11
Footnotes
Paper previously presented, in part, in abstract form at: Hydrocephalus 2017, Ninth Meeting of the International Society for Hydrocephalus and CSF Disorders, September 23–25, 2017; Kobe, Japan.
Indicates open access to non-subscribers at www.ajnr.org
References
- Received July 5, 2018.
- Accepted after revision October 2, 2018.
- © 2019 by American Journal of Neuroradiology
Jump to section
Related Articles
Cited By...
- No citing articles found.